Standard Error of the Mean (S.E. Mean) hay sai số chuẩn của giá trị trung bình là một chỉ số thống kê dùng để đo lường mức độ không chắc chắn của giá trị trung bình của một mẫu so với giá trị trung bình thực sự của tổng thể. S.E. Mean giúp chúng ta đánh giá mức độ sai lệch mà giá trị trung bình mẫu có thể có khi ta lấy nhiều mẫu từ cùng một tổng thể.
Standard Error of the Mean (S.E. Mean) là gì?
- E. Mean là thước đo cho sự phân tán của các giá trị trung bình mẫu nếu chúng ta thực hiện nhiều lần lấy mẫu ngẫu nhiên từ cùng một tổng thể.
- E. Mean cho biết trung bình mẫu (sample mean) sai khác bao nhiêu so với trung bình tổng thể (population mean).
- Công thức tính S.E. Mean:
Trong đó:
- S là độ lệch chuẩn (Standard Deviation) của mẫu.
- n là kích thước mẫu (Sample Size).
Tầm quan trọng của S.E. Mean
- Độ chính xác của mẫu:
- E. Mean cho biết độ chính xác mà trung bình mẫu ước tính trung bình tổng thể. Sai số chuẩn nhỏ cho thấy trung bình mẫu có khả năng gần với trung bình tổng thể, từ đó nâng cao độ chính xác của nghiên cứu.
- Tính hợp lý của nghiên cứu lâm sàng:
- Trong các nghiên cứu lâm sàng hoặc khoa học, việc đảm bảo rằng mẫu phản ánh chính xác tổng thể là rất quan trọng để có thể khái quát hóa các phát hiện. S.E. Mean giúp đánh giá điều này bằng cách cho thấy trung bình của mẫu có thể chênh lệch bao nhiêu so với trung bình thực sự của tổng thể.
- Đánh giá sai số lấy mẫu:
- Mỗi mẫu đều có một mức độ sai số lấy mẫu nhất định – sự chênh lệch giữa trung bình của mẫu và trung bình của tổng thể. S.E. Mean thấp chỉ ra rằng sai số lấy mẫu là thấp, qua đó xác nhận rằng mẫu là đại diện tốt của tổng thể.
- Tăng độ tin cậy của kết luận:
- Với S.E. Mean thấp, khoảng tin cậy xung quanh trung bình của mẫu sẽ hẹp hơn, có nghĩa là bạn có thể tự tin hơn rằng trung bình thực sự của tổng thể nằm trong một khoảng xác định. Điều này củng cố tính hợp lệ của bất kỳ kết luận nào được rút ra từ nghiên cứu.
Tính S.E. Mean trong SPSS
Để tính S.E. Mean trong SPSS, bạn có thể làm theo các bước sau:
Nhập dữ liệu: Sau khi nhập dữ liệu của bạn vào SPSS, chọn biến mà bạn muốn tính giá trị trung bình và sai số chuẩn.

Tính toán:
-
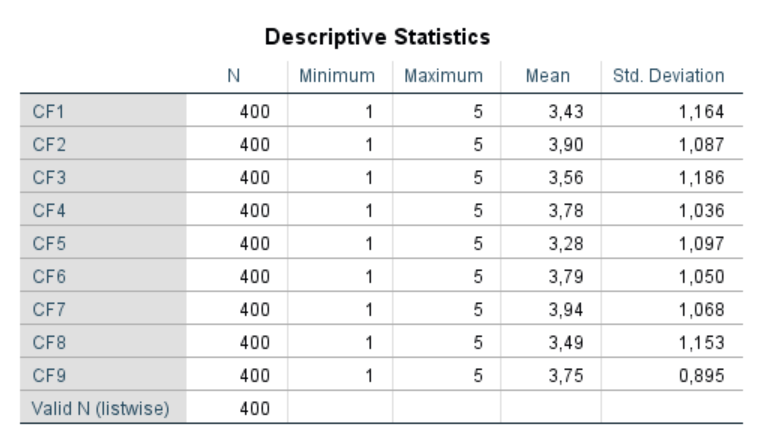
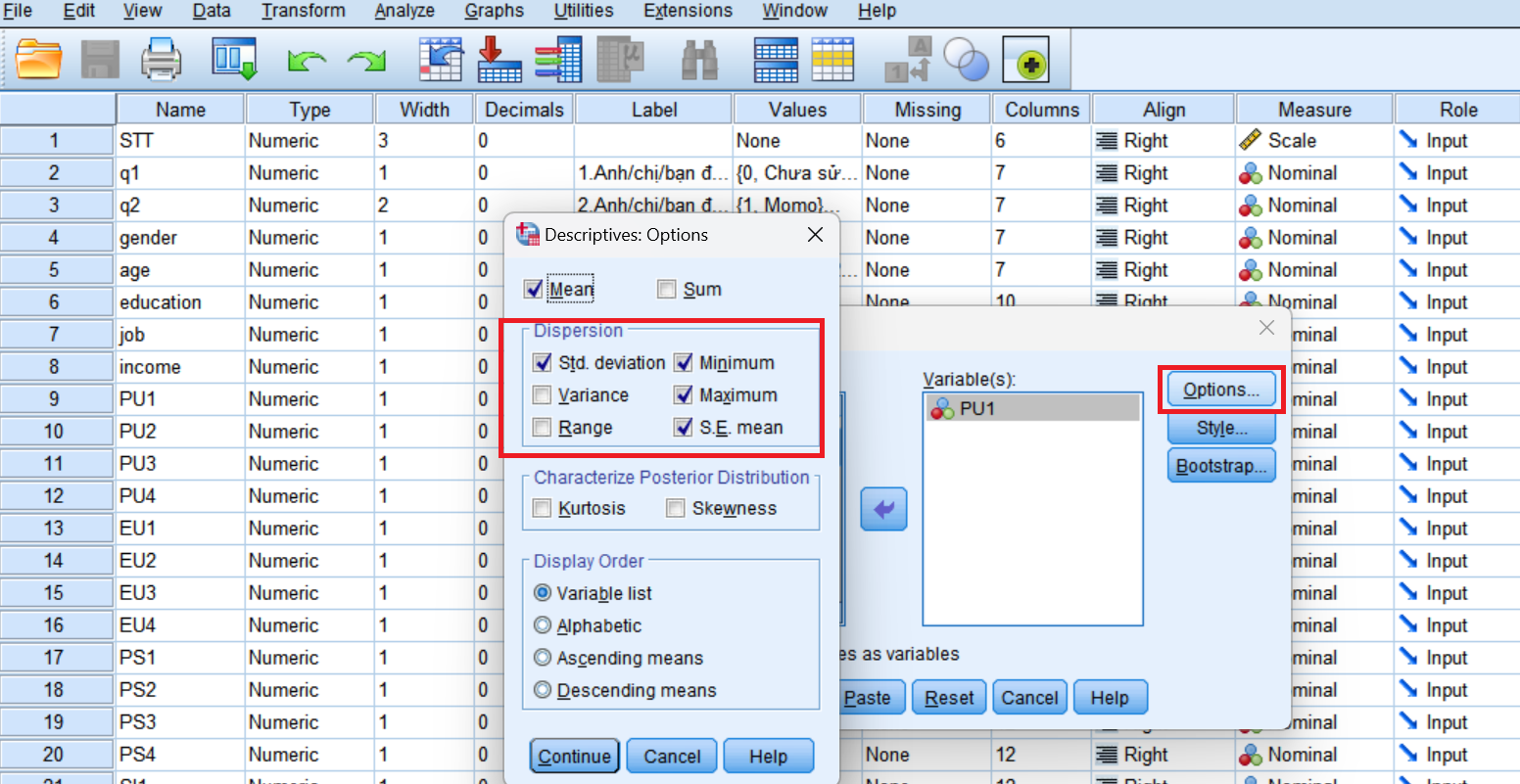
- Vào Analyze > Descriptive Statistics > Descriptives.
- Chọn biến mà bạn muốn phân tích, sau đó nhấn OK.
Kết quả: SPSS sẽ hiển thị bảng kết quả, trong đó có giá trị Mean (trung bình) và S.E. Mean (Standard Error of Mean).
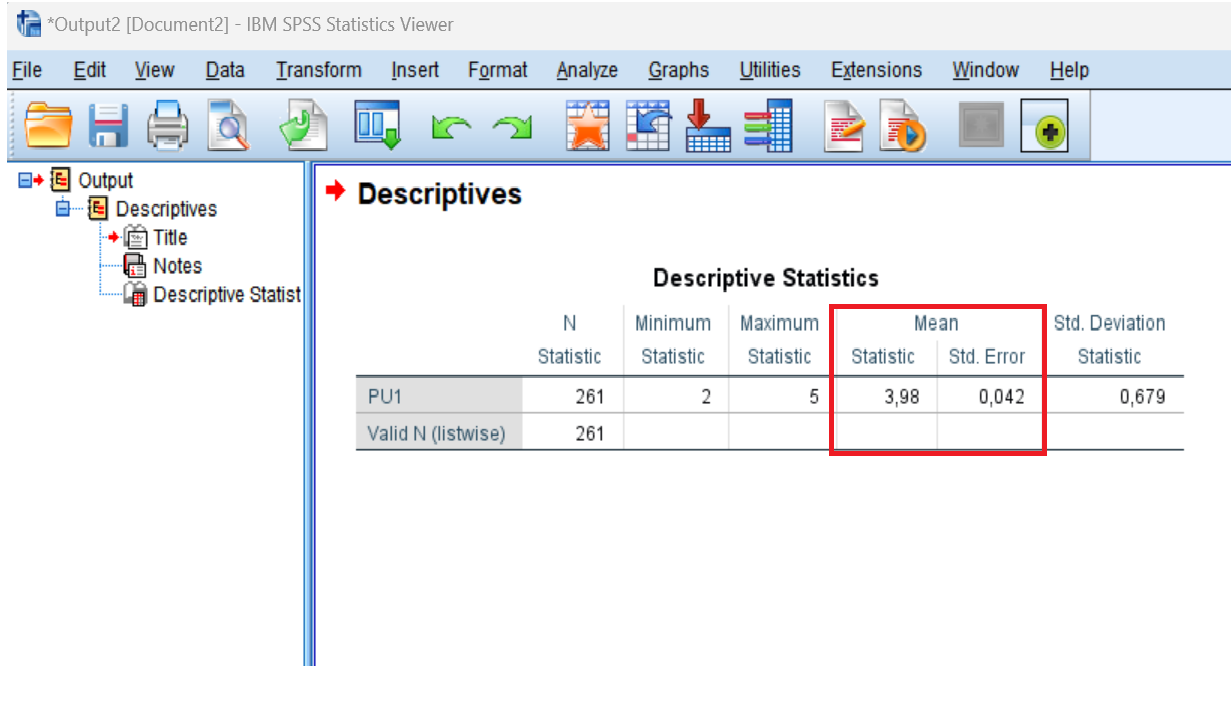
Ý nghĩa của S.E. Mean
- S.E. Mean giúp ước lượng mức độ tin cậy của giá trị trung bình mẫu. Nếu S.E. Mean nhỏ, điều đó có nghĩa là giá trị trung bình mẫu gần với giá trị trung bình tổng thể. Ngược lại, nếu S.E. Mean lớn, điều đó cho thấy có nhiều biến động hơn trong các giá trị trung bình của mẫu.
- S.E. Mean còn được sử dụng để tính toán các khoảng tin cậy (confidence intervals) cho giá trị trung bình, giúp dự đoán khoảng giá trị mà giá trị trung bình tổng thể có khả năng nằm trong khoảng đó với một mức độ tin cậy nhất định (thường là 95% hoặc 99%).
Quan hệ giữa độ lệch chuẩn và sai số chuẩn của giá trị trung bình
- Độ lệch chuẩn (Standard Deviation, SD) đo lường mức độ phân tán của các điểm dữ liệu trong một mẫu. Nó cho biết sự khác biệt giữa các giá trị trong dữ liệu với giá trị trung bình của mẫu.
- Sai số chuẩn của giá trị trung bình (S.E. Mean) đo lường mức độ sai lệch của trung bình mẫu với trung bình tổng thể. S.E. Mean phụ thuộc vào độ lệch chuẩn và kích thước mẫu. Khi kích thước mẫu tăng, S.E. Mean giảm, điều này có nghĩa là trung bình mẫu sẽ ngày càng chính xác hơn khi ước lượng trung bình tổng thể.
Tóm lại:
- S.D. đo lường sự biến động của từng điểm dữ liệu trong mẫu.
- S.E.Mean đo lường sự biến động của trung bình mẫu.
Ví dụ: Với cùng một giá trị độ lệch chuẩn, nếu kích thước mẫu tăng, sai số chuẩn sẽ giảm, dẫn đến sự ước lượng trung bình tổng thể chính xác hơn.
Kết luận
S.E. Mean là thước đo quan trọng để đánh giá độ tin cậy của giá trị trung bình mẫu.
Nó liên quan mật thiết đến độ lệch chuẩn và kích thước mẫu, và được sử dụng rộng rãi trong các nghiên cứu để xác định mức độ chính xác khi ước lượng giá trị trung bình tổng thể từ một mẫu.







