PHÂN TÍCH TƯƠNG QUAN PEARSON TRÊN SPSS

Phân tích tương quan là một kỹ thuật thống kê quan trọng, được sử dụng rộng rãi trong nghiên cứu khoa học để kiểm tra mối quan hệ giữa các biến số. Một trong những phương pháp phổ biến nhất để xác định mối quan hệ tuyến tính giữa hai biến là hệ số tương quan Pearson (Pearson correlation coefficient, ký hiệu r). Trong bài viết này, chúng ta sẽ tìm hiểu về hệ số tương quan Pearson, mục đích của việc chạy phân tích này, các bước thực hiện trong phần mềm SPSS, và cách đọc kết quả phân tích.

1. Khái niệm tương quan

Người ta sử dụng một số thống kê có tên là hệ số tương quan Pearson (ký hiệu r) để lượng hóa mức độ chặt chẽ của mối liên hệ tuyến tính giữa 2 biến định lượng (lưu ý rằng Pearson chỉ xét mối liên hệ tuyến tính, không đánh giá các mối liên hệ phi tuyến). Trong tương quan Pearson không có sự phân biệt vai trò giữa 2 biến, tương quan giữa biến độc lập với biến độc lập cũng như giữa biến độc lập với biến phụ thuộc.

2. Mục đích của việc chạy tương quan Pearson

2.1. Kiểm tra mối quan hệ tuyến tính

Mục đích chính của việc thực hiện phân tích tương quan Pearson là để kiểm tra mối quan hệ tuyến tính chặt chẽ giữa biến phụ thuộc và các biến độc lập. Mối quan hệ này rất quan trọng vì nó là điều kiện tiên quyết để tiến hành phân tích hồi quy. Nếu các biến không có mối tương quan, việc xây dựng mô hình hồi quy sẽ không chính xác và kết quả phân tích có thể bị sai lệch.

2.2. Nhận diện đa cộng tuyến

Ngoài việc xác định mối quan hệ giữa biến phụ thuộc và biến độc lập, phân tích tương quan Pearson còn giúp nhận diện vấn đề đa cộng tuyến. Đa cộng tuyến xảy ra khi các biến độc lập có mối tương quan mạnh với nhau, dẫn đến việc làm tăng độ sai lệch của các ước lượng hồi quy. Để nhận diện đa cộng tuyến, chúng ta có thể kiểm tra hệ số VIF (Variance Inflation Factor) trong quá trình phân tích hồi quy.

3. Các tiêu chí về tương quan

Tương quan Pearson r có giá trị dao động từ -1 đến 1:

Nếu r càng tiến về 1, -1: tương quan tuyến tính càng mạnh, càng chặt chẽ. Tiến về 1 là tương quan dương, tiến về -1 là tương quan âm.
Nếu r càng tiến về 0: tương quan tuyến tính càng yếu.
Nếu r = 1: tương quan tuyến tính tuyệt đối, khi biểu diễn trên đồ thị phân tán, các điểm biểu diễn sẽ nhập lại thành 1 đường thẳng.

Nếu r = 0: không có mối tương quan tuyến tính. Lúc này sẽ có 2 tình huống xảy ra. Một, không có một mối liên hệ nào giữa 2 biến. Hai, giữa chúng có mối liên hệ phi tuyến

4. Hướng dẫn các bước phân tích hệ số tương quan pearson trong SPSS

Để thực hiện phân tích tương quan Pearson bivariate trong SPSS, nhấp vào Analyze > Correlate > Bivariate.

Sau đó tiếp tục chọn các biến (biến đại diện) đưa vào khung Variables

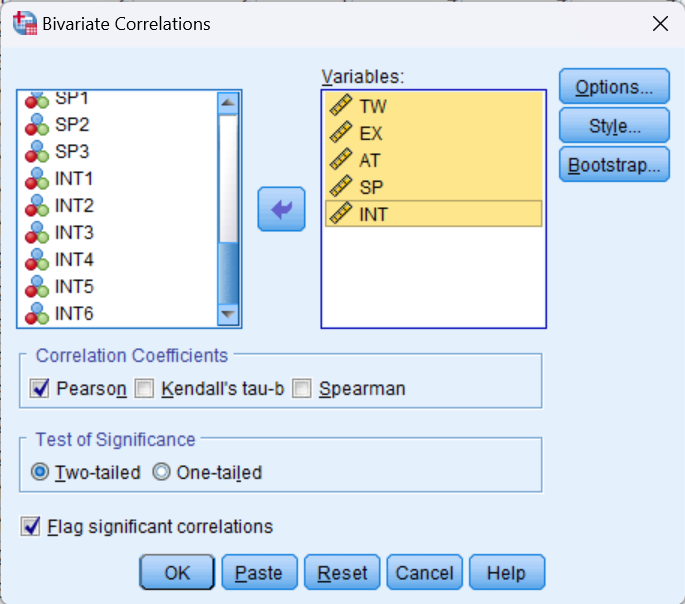
Variables: Các biến được sử dụng trong phân tích tương quan Pearson bivariate. Bạn phải chọn ít nhất hai biến liên tục, nhưng có thể chọn nhiều hơn. Phép kiểm định sẽ tạo ra các hệ số tương quan cho từng cặp biến trong danh sách này.

Correlation Coefficients: Có nhiều loại hệ số tương quan. Theo mặc định, Pearson được chọn. Chọn Pearson sẽ cung cấp các thống kê kiểm định cho phân tích tương quan Pearson bivariate.

Test of Significance: Chọn kiểm định hai phía (Two-tailed) hoặc một phía (One-tailed), tùy thuộc vào kiểm định ý nghĩa mà bạn mong muốn. SPSS mặc định sử dụng kiểm định hai phía.

Flag significant correlations: Chọn tùy chọn này sẽ bao gồm dấu hoa thị (**) bên cạnh các tương quan có ý nghĩa thống kê trong kết quả đầu ra. Theo mặc định, SPSS đánh dấu mức ý nghĩa thống kê ở alpha = 0,05 và alpha = 0,01, nhưng không đánh dấu ở mức alpha = 0,001 (được coi là alpha = 0,01).

Options: Nhấp vào Options sẽ mở cửa sổ cho phép bạn chỉ định các thống kê nào cần bao gồm (ví dụ: Giá trị trung bình và độ lệch chuẩn, độ lệch tích chéo và hiệp phương sai) và cách xử lý giá trị thiếu (ví dụ: Loại trừ trường hợp theo cặp hoặc loại trừ trường hợp theo danh sách). Lưu ý rằng tùy chọn theo cặp/danh sách không ảnh hưởng đến tính toán nếu bạn chỉ nhập hai biến, nhưng có thể tạo ra sự khác biệt lớn nếu bạn nhập ba hoặc nhiều biến vào quy trình tương quan.

5. Đọc kết quả phân tích tương quan

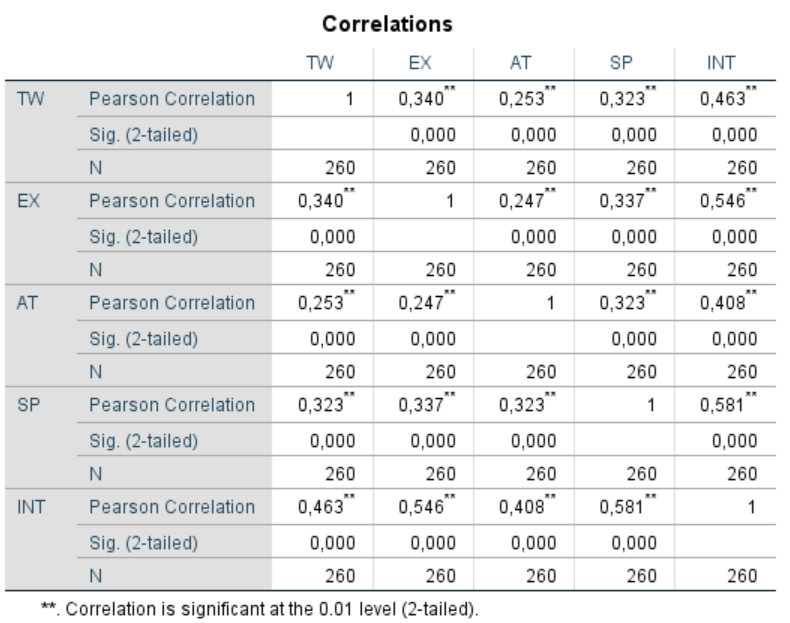
Sau khi thực hiện phân tích, SPSS sẽ hiển thị một bảng kết quả chứa hệ số tương quan Pearson và các thông tin liên quan. Dưới đây là cách đọc và diễn giải kết quả phân tích:

Giải thích khái niệm

Hàng Pearson Correlation là giá trị r để xem xét sự tương thuận hay nghịch, mạnh hay yếu giữa 2 biến.
Hàng Sig. (2-tailed) là sig kiểm định xem mối tương quan giữa 2 biến là có ý nghĩa hay không. Sig < 0.05, tương quan có ý nghĩa; sig > 0.05, tương quan không có ý nghĩa.
Hàng N hiển thị cỡ mẫu của tập dữ liệu.

5.1. Hệ số tương quan Pearson (r)

Hệ số tương quan Pearson (r): Giá trị này cho biết mức độ và hướng của mối quan hệ tuyến tính giữa hai biến. Ví dụ, r = 0.8 cho thấy mối quan hệ tuyến tính dương mạnh, trong khi r = -0.5 cho thấy mối quan hệ tuyến tính âm trung bình.

5.2. Mức ý nghĩa thống kê (p-value)

Mức ý nghĩa thống kê (p-value): Giá trị p cho biết mức độ tin cậy của mối quan hệ tuyến tính. Nếu p-value nhỏ hơn mức ý nghĩa chọn trước (thường là 0.05), mối quan hệ tuyến tính giữa hai biến là có ý nghĩa thống kê. Ngược lại, nếu p-value lớn hơn 0.05, không có đủ bằng chứng để khẳng định mối quan hệ này.

5.3. Hướng dẫn diễn giải kết quả

Khi đọc kết quả, bạn cần xem xét cả giá trị của r và p-value để đưa ra kết luận chính xác. Dưới đây là một ví dụ minh họa:

Nếu r = 0.6 và p-value < 0.05: Điều này cho thấy có mối quan hệ tuyến tính dương vừa phải giữa hai biến và mối quan hệ này có ý nghĩa thống kê.
Nếu r = -0.3 và p-value > 0.05: Điều này cho thấy có mối quan hệ tuyến tính âm yếu giữa hai biến và mối quan hệ này không có ý nghĩa thống kê.

Kết luận: Phân tích tương quan Pearson là một công cụ quan trọng trong nghiên cứu khoa học, giúp xác định mối quan hệ tuyến tính giữa các biến. Điều này hỗ trợ nhà nghiên cứu xây dựng mô hình hồi quy chính xác và tin cậy. Việc nhận diện và giải quyết đa cộng tuyến cũng là một bước quan trọng để đảm bảo tính chính xác của kết quả phân tích.