1.Tổng quan về hồi quy nhị phân
Hồi quy nhị phân (Binary Logistic Regression) là một kỹ thuật thống kê được sử dụng để ước lượng xác suất xảy ra của một sự kiện khi biến phụ thuộc ở dạng nhị phân (tức có hai giá trị, thường là 0 và 1). Trong nhiều hiện tượng tự nhiên, chúng ta cần dự đoán khả năng xảy ra của các sự kiện quan trọng. Ví dụ như: liệu một sản phẩm mới có được chấp nhận hay không, khách hàng vay có thể trả nợ hay không, hoặc một người tiêu dùng có mua hàng hay không. Những biến nghiên cứu có hai biểu hiện như vậy được gọi là biến thay phiên (dichotomous), và khi chúng được mã hóa thành các giá trị 0 và 1, chúng trở thành biến nhị phân.
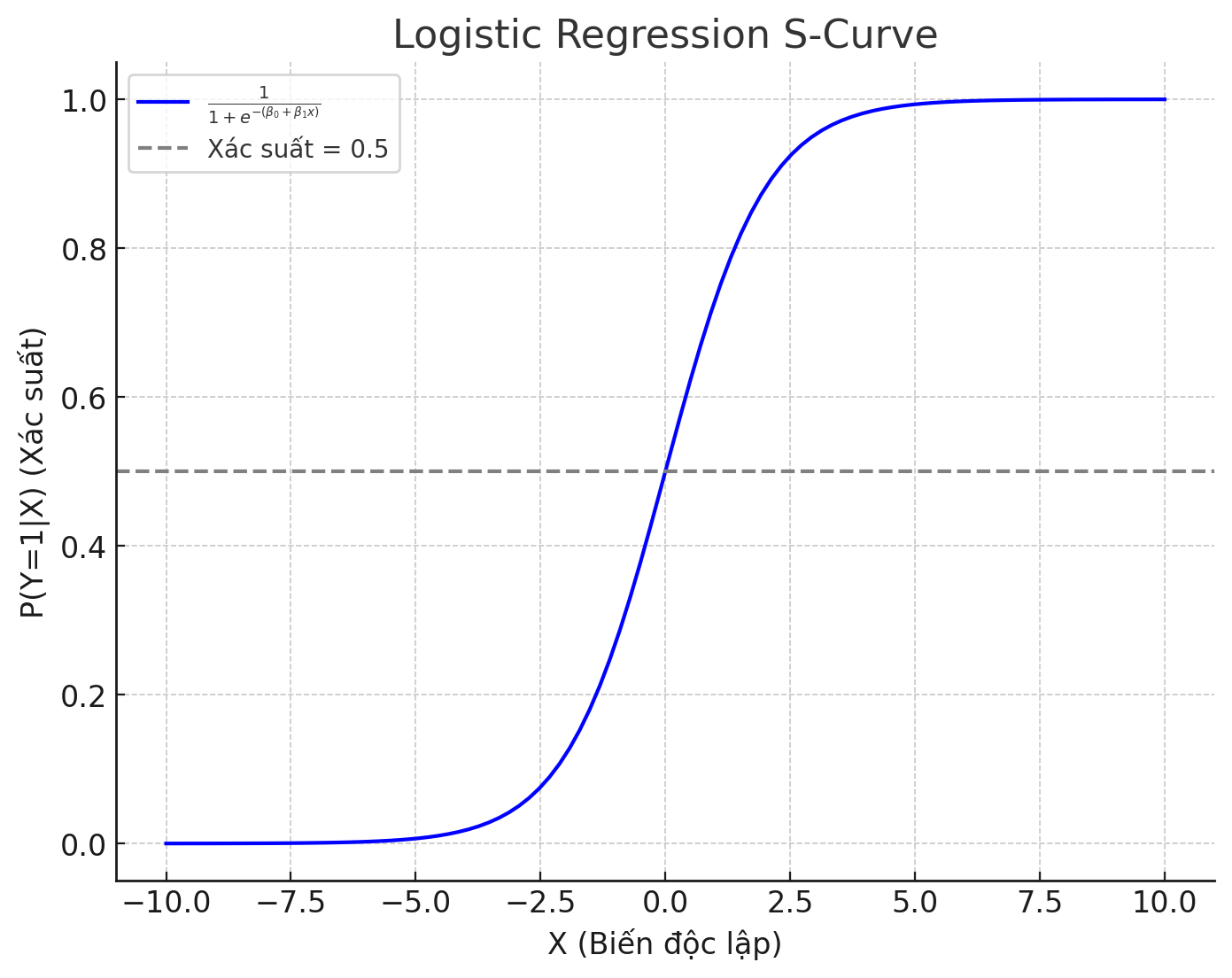
Đây là biểu đồ đường cong chữ S của mô hình hồi quy logistic. Trục hoành (X) đại diện cho biến độc lập, còn trục tung (P(Y=1|X)) biểu thị xác suất sự kiện xảy ra (Y=1) dựa trên giá trị của X. Đường cong logistic này cho thấy xác suất tăng dần khi giá trị của X tăng, với điểm giữa tại xác suất 0.5.
Bạn có thể thấy rằng ở mức X thấp, xác suất gần bằng 0, và khi X tăng lên, xác suất dần tiếp cận 1, tạo nên đường cong chữ S đặc trưng.
Phương trình hồi quy logistic là:
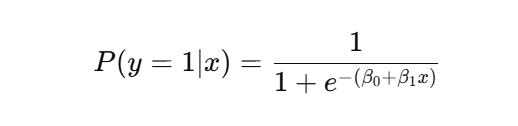
Trong đó, P(y=1∣x)P(y = 1 | x)P(y=1∣x) là xác suất mà biến phụ thuộc yyy bằng 1 khi biết giá trị của biến độc lập x, và β0, β1 là các tham số hồi quy.
2. Tại sao không dùng hồi quy tuyến tính?
Biến nhị phân không thể được phân tích bằng hồi quy tuyến tính truyền thống vì các giả định của mô hình tuyến tính không được đáp ứng. Cụ thể, khi biến phụ thuộc chỉ có hai biểu hiện, nó sẽ không tuân theo phân phối chuẩn mà thay vào đó là phân phối nhị thức. Điều này khiến các kiểm định thống kê trong hồi quy tuyến tính trở nên không còn hiệu lực. Một vấn đề khác là giá trị dự đoán từ hồi quy tuyến tính có thể vượt ra ngoài khoảng từ 0 đến 1, điều này không phù hợp để diễn giải như xác suất.
3. Kiểm định độ phù hợp tổng quát
Trong hồi quy nhị phân, kiểm định Chi-square được sử dụng để kiểm tra giả thuyết H0 rằng các hệ số hồi quy của các biến độc lập đều bằng 0. Kết quả của kiểm định này được thể hiện trong bảng Omnibus Tests of Model Coefficients của phần mềm SPSS. Nếu giá trị Sig. nhỏ hơn 0.05, chúng ta bác bỏ giả thuyết H0, tức là mô hình có ý nghĩa thống kê.
4. Kiểm định ý nghĩa của các hệ số hồi quy
Giả thuyết kiểm định trong hồi quy nhị phân là hệ số hồi quy khác không. Nếu hệ số hồi quy B0 và B1 đều bằng 0 thì tỷ lệ chênh lệch giữa các xác suất sẽ bằng 1, tức xác suất để sự kiện xảy ra hay không xảy ra như nhau, lúc đó mô hình hồi quy của chúng ta vô dụng trong việc dự đoán.
Để kiểm định ý nghĩa của hệ số hồi quy trong hồi quy nhị phân, đại lượng Wald Chi-square được sử dụng. Wald Chi-square được tính bằng cách lấy giá trị ước lượng của hệ số hồi quy chia cho sai số chuẩn của hệ số đó, sau đó bình phương kết quả. Giá trị Sig. của kiểm định Wald được sử dụng để đánh giá ý nghĩa thống kê của từng biến độc lập trong mô hình.
5. Kiểm định độ phù hợp của mô hình
Mục tiêu của kiểm định này là xác định liệu có mối quan hệ tuyến tính giữa các biến độc lập và biến phụ thuộc hay không. Nếu có ít nhất một hệ số hồi quy khác 0, mô hình được coi là phù hợp. Giá trị Prob > Chi2 được xem xét, nếu giá trị này ≤ 0.05 (với mức độ tin cậy ít nhất 95%), mô hình được xem là có mối quan hệ tuyến tính và phù hợp.
6. Kiểm định mức độ giải thích của mô hình
Kiểm định mức độ giải thích của mô hình sử dụng thước đo Pseudo R2 nhằm đánh giá bao nhiêu phần trăm sự thay đổi của biến phụ thuộc được giải thích bởi các biến độc lập. Đây là một thước đo quan trọng để đánh giá khả năng dự đoán của mô hình.
7. Phương pháp đưa biến độc lập vào phương trình hồi quy
Có nhiều phương pháp để đưa các biến độc lập vào mô hình hồi quy nhị phân. Các phương pháp phổ biến bao gồm: nhập toàn bộ các biến cùng lúc (Enter), hoặc sử dụng các phương pháp từng bước như Forward Selection và Backward Elimination để chọn lọc các biến có ý nghĩa thống kê cao nhất.
Kết luận
Hồi quy nhị phân là một công cụ mạnh mẽ trong việc dự đoán các sự kiện có biến phụ thuộc dạng nhị phân. Mô hình này không chỉ giúp chúng ta dự đoán xác suất xảy ra của một sự kiện mà còn cung cấp thông tin về mức độ ảnh hưởng của các yếu tố khác nhau lên biến phụ thuộc. Việc hiểu rõ các kiểm định như Chi-square và Wald, cũng như các thước đo đánh giá mô hình như Pseudo R2, sẽ giúp nâng cao chất lượng phân tích và khả năng dự đoán của mô hình hồi quy nhị phân.







