PHÂN TÍCH DỮ LIỆU BẰNG HỒI QUY NHỊ PHÂN TRÊN SPSS

Hồi quy logistic nhị phân là một kỹ thuật phân tích thống kê dùng để mô hình hóa mối quan hệ giữa một biến phụ thuộc nhị phân (chỉ nhận giá trị 0 hoặc 1) và một hoặc nhiều biến độc lập. Phương pháp này đặc biệt hữu ích trong việc dự đoán xác suất của một sự kiện nhị phân dựa trên các yếu tố ảnh hưởng.

Phần mềm SPSS, một công cụ mạnh mẽ trong phân tích thống kê, cung cấp các chức năng tiện ích để thực hiện hồi quy logistic nhị phân. Quy trình phân tích bao gồm việc nhập dữ liệu, chọn biến phụ thuộc và biến độc lập, sau đó sử dụng mô hình hồi quy logistic để đánh giá tác động của các biến độc lập lên xác suất xảy ra của sự kiện quan tâm.

Kết quả phân tích sẽ cung cấp các hệ số hồi quy, cho phép nhà nghiên cứu hiểu rõ hơn về mối quan hệ giữa các biến và đưa ra các dự đoán chính xác hơn.

Các giả định của hồi quy nhị phân

Hồi quy logistic không yêu cầu mối quan hệ tuyến tính giữa biến phụ thuộc và các biến độc lập.

Các biến độc lập trong mô hình không nhất thiết phải có thang đo khoảng, không cần tuân theo phân phối chuẩn, không cần liên hệ tuyến tính và cũng không yêu cầu phương sai bằng nhau giữa các nhóm.

Đặc biệt, tính đồng nhất của phương sai (homoscedasticity) không phải là điều kiện cần thiết. Ngoài ra, các sai số (hay phần dư) trong mô hình hồi quy logistic không cần phải tuân theo phân phối chuẩn.

Trong hồi quy nhị phân logistic, biến phụ thuộc không được đo lường theo thang đo khoảng hay tỷ lệ. Thay vào đó, biến phụ thuộc phải là biến nhị phân (dichotomous) có hai loại (ví dụ: 0 và 1) đối với mô hình hồi quy logistic nhị phân. Các loại của biến phụ thuộc phải là các nhóm loại trừ lẫn nhau và toàn diện, tức là mỗi trường hợp chỉ có thể thuộc về một nhóm và tất cả các trường hợp phải thuộc vào một trong hai nhóm.

Yêu cầu về cỡ mẫu

Hồi quy logistic yêu cầu cỡ mẫu lớn hơn so với hồi quy tuyến tính, vì các hệ số hồi quy được ước lượng bằng phương pháp ước lượng hợp lý tối đa (Maximum Likelihood Estimation), đòi hỏi mẫu lớn để có thể ước lượng chính xác. Theo Field (2013), cỡ mẫu tối thiểu được khuyến nghị là 50 trường hợp cho mỗi biến dự đoán.

Hosmer, Lemeshow và Sturdivant (2013) đề xuất một cỡ mẫu tối thiểu là 10 quan sát cho mỗi biến độc lập trong mô hình, tuy nhiên, họ cũng khuyến cáo rằng nếu có thể, nên cố gắng đạt 20 quan sát cho mỗi biến. Leblanc và Fitzgerald (2000) thậm chí đề nghị tối thiểu 30 quan sát cho mỗi biến độc lập để đảm bảo độ tin cậy của kết quả phân tích.

Ví dụ tham khảo

Trong ví dụ này, chúng ta sẽ sử dụng hồi quy logistic nhị phân để dự đoán tình trạng nghèo của các hộ gia đình ở tỉnh Bến Tre dựa trên các biến độc lập được đo trên thang đo khoảng hoặc phân loại. Biến phụ thuộc (DV) là tình trạng nghèo của hộ gia đình, được mã hóa dưới dạng nhị phân: có giá trị bằng 1 (nếu hộ gia đình nghèo) và bằng 0 (cho tất cả các hộ gia đình khác)

Mục tiêu nghiên cứu: Dựa vào số liệu khảo sát về nghèo của 200 hộ gia đình ở thành phố Bến Tre, hàm hồi quy Binary Logistic về tác động của nguồn vốn con người đến nghèo của hộ gia đình dựa trên các biến độc lập như sau: Trình độ chuyên môn; Học vấn chủ hộ; Sức khõe; Kỹ năng cụ thể

Bảng: Mô tả các biến và kỳ vọng dấu trong mô hình hồi quy

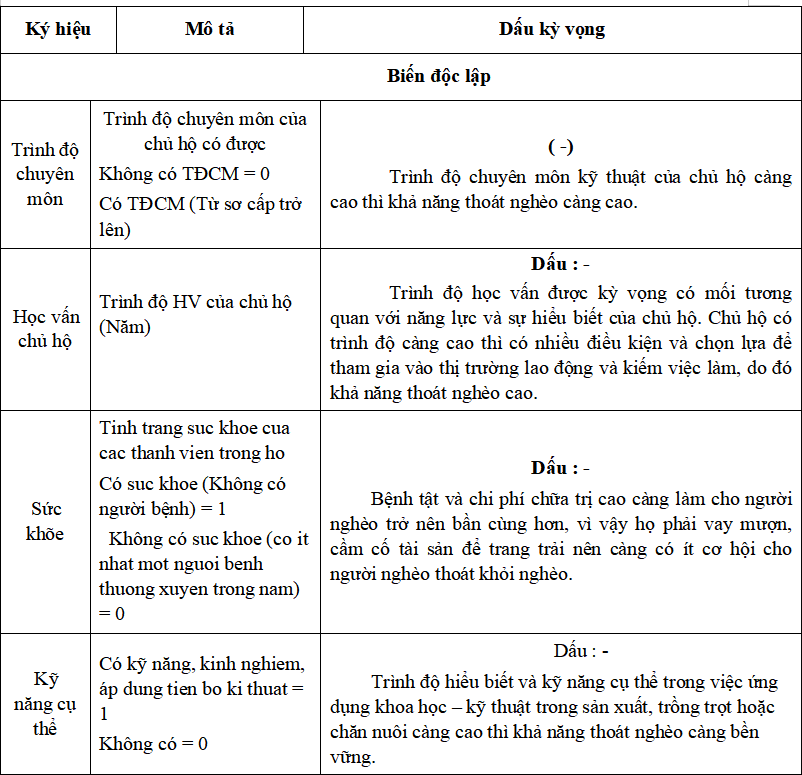
Hồi quy logistic nhị phân sẽ được sử dụng để đánh giá xác suất mà một hộ gia đình rơi vào tình trạng nghèo, dựa trên các yếu tố như trình độ chuyên môn, học vấn của chủ hộ, sức khỏe, và kỹ năng cụ thể. Mục đích là kiểm tra xem những yếu tố nào trong nguồn vốn con người có tác động đáng kể đến khả năng hộ gia đình thuộc nhóm nghèo.

Các giả thuyết của nghiên cứu:

Trình độ chuyên môn cao hơncó thể làm giảm xác suất một hộ gia đình rơi vào tình trạng nghèo.
Học vấn của chủ hộ cao hơncó thể giúp hộ gia đình tránh khỏi nghèo đói.
Tình trạng sức khỏe tốt hơncủa chủ hộ hoặc thành viên gia đình có thể dẫn đến việc tăng thu nhập và giảm khả năng nghèo.
Kỹ năng cụ thể cao hơncó thể giúp chủ hộ tìm kiếm việc làm tốt hơn hoặc nâng cao khả năng kiếm sống, từ đó giảm nghèo.

Trong quá trình phân tích, các hệ số hồi quy (beta) sẽ được ước lượng để xác định mức độ ảnh hưởng của từng yếu tố (trình độ chuyên môn, học vấn, sức khỏe, kỹ năng cụ thể) đến xác suất rơi vào tình trạng nghèo. Các hệ số này cho biết mỗi biến độc lập ảnh hưởng như thế nào đến tỷ lệ odds (tỷ lệ xác suất thuộc nhóm nghèo so với không nghèo).

Phân tích này sẽ cung cấp cái nhìn sâu sắc về vai trò của nguồn vốn con người trong việc ảnh hưởng đến tình trạng nghèo của các hộ gia đình tại Bến Tre. Kết quả có thể được sử dụng để đưa ra các khuyến nghị chính sách nhằm cải thiện giáo dục, sức khỏe, và phát triển kỹ năng cho các hộ gia đình nghèo, từ đó giúp giảm nghèo hiệu quả hơn.

Hướng dẫn cách chạy hồi quy nhị phân trên SPSS

 Bước  1: Trong SPSS, chọn Analyze -> Regression -> Binary Logistic

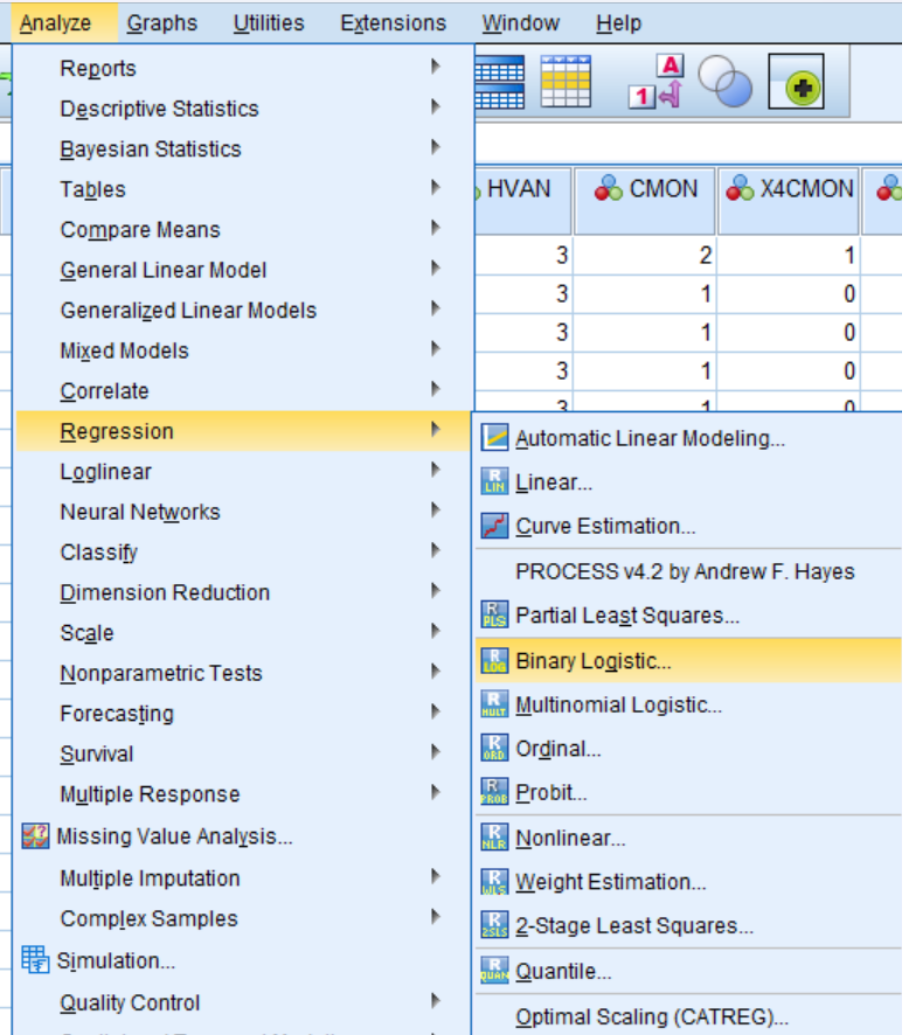
Bước 2: Xuất hiện hộp thoại Logistic Regression

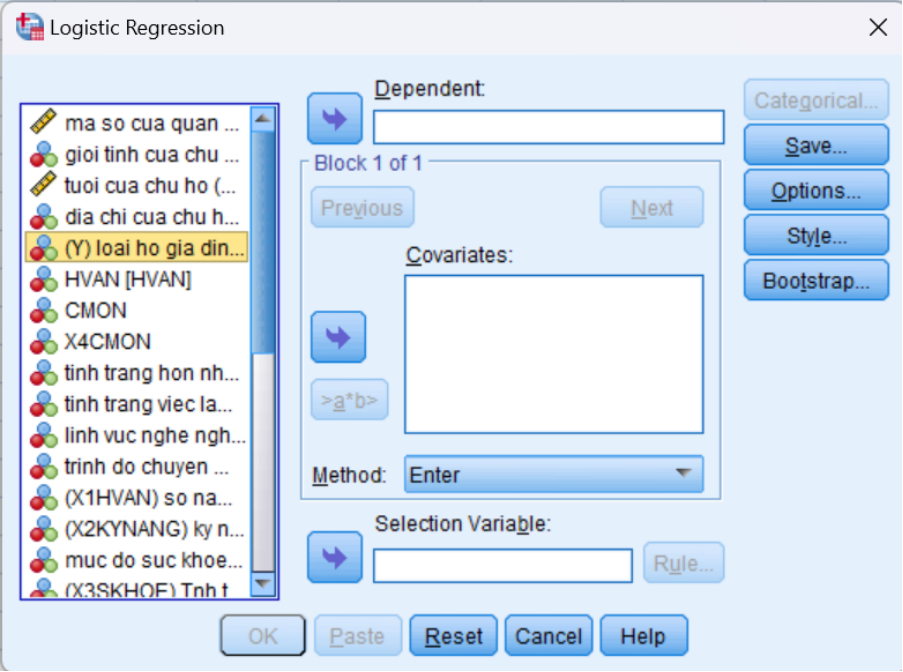
Sau khi bạn chọn lệnh hồi quy logistic nhị phân trong phần mềm SPSS, hộp thoại Logistic Regression sẽ xuất hiện. Đây là nơi bạn sẽ thiết lập các biến phụ thuộc (DV) và biến độc lập (IV) cho phân tích của mình. Dưới đây là các bước để cấu hình hộp thoại:

Bước 3: Đưa các biến vào các ô tương ứng

Biến phụ thuộc (Dependent Variable):
Chọn biến đại diện cho tình trạng nghèo của hộ gia đình (ví dụ: “Tình trạng nghèo”). Đây là biến nhị phân với hai giá trị (1 = nghèo, 0 = không nghèo).
Di chuyển biến này vào ô Dependenttrong hộp thoại.
Biến độc lập (Covariates):
Chọn các biến độc lập (ví dụ: “Trình độ chuyên môn”, “Học vấn của chủ hộ”, “Sức khỏe”, “Kỹ năng cụ thể”) từ danh sách các biến.
Di chuyển các biến này vào ô Covariates.

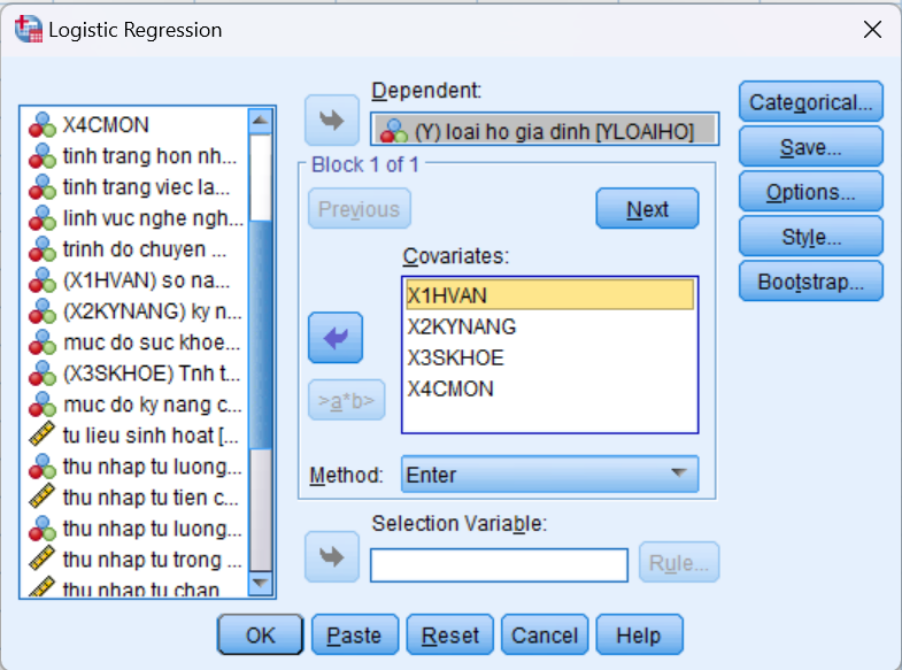
Bước 4: Chọn Options và đánh dấu các tùy chọn kiểm định Hosmer-Lemeshow goodness-of-fit và CI cho exp(B)

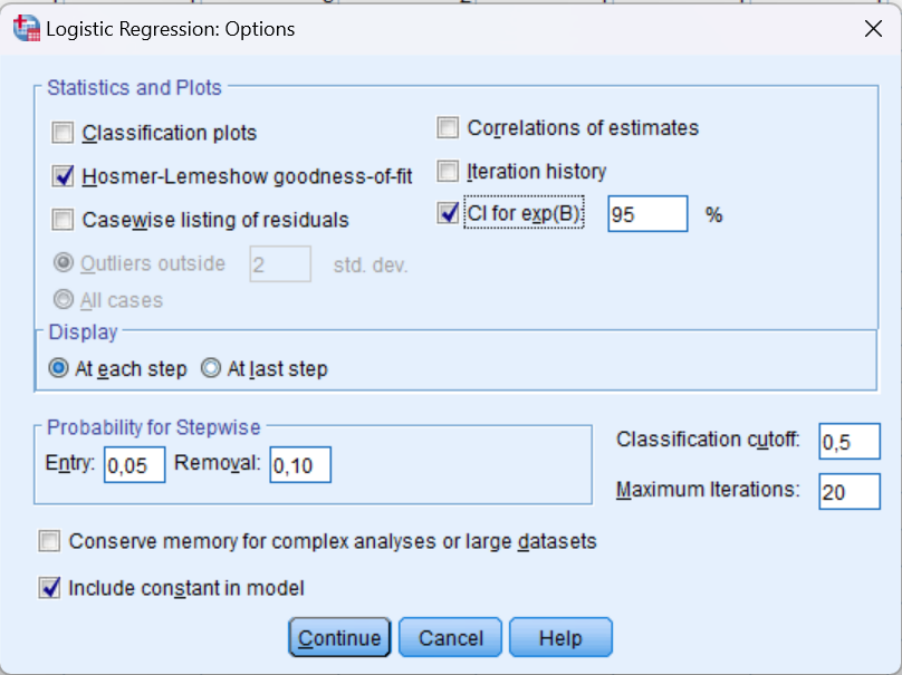
Kiểm định Hosmer-Lemeshow goodness-of-fit:

Trong hộp thoại Options, bạn sẽ thấy nhiều tùy chọn kiểm định cho mô hình.
Đánh dấu vào ô Hosmer-Lemeshow goodness-of-fit. Đây là một kiểm định quan trọng để đánh giá mức độ phù hợp của mô hình hồi quy logistic. Nó giúp kiểm tra xem mô hình dự đoán có phù hợp với dữ liệu thực tế hay không.

Khoảng tin cậy cho exp(B):

Để nhận thông tin về khoảng tin cậy (CI) cho exp(B), hãy đánh dấu ô Confidence Interval (CI) for exp(B).
Khoảng tin cậy này cung cấp mức độ chính xác của hệ số odds ratio, cho phép bạn đánh giá biến số độc lập ảnh hưởng đến xác suất của biến phụ thuộc như thế nào trong khoảng tin cậy 95%.

Bước 5: Nhấn Continue, sau đó nhấn tiếp OK

Nhấn Continue:

Sau khi đánh dấu các tùy chọn trên, nhấn Continue để trở về hộp thoại chính.

OK:

Sau đó, nhấn OK trong hộp thoại chính để chạy phân tích hồi quy logistic.

Báo cáo kết quả hồi quy nhị phân

Dưới đây là tóm tắt kết quả hồi quy nhị phân của 200 quan sát

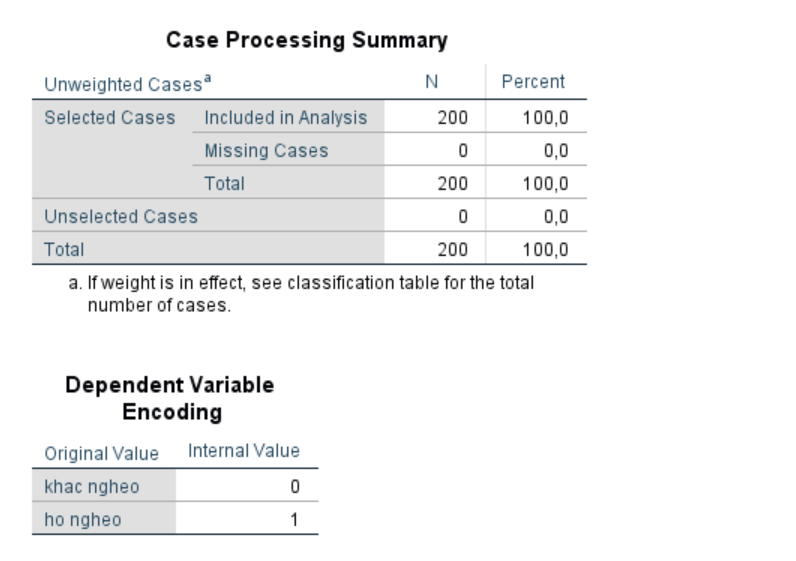
Case Processing Summary:

Included in Analysis: Có 200 trường hợp được đưa vào phân tích (100% tổng số trường hợp).
Missing Cases: Không có trường hợp bị thiếu (0%).
Total: Tổng số trường hợp là 200 (100%).
Unselected Cases: Không có trường hợp nào bị loại bỏ (0%).

Dependent Variable Encoding:

khac ngheo(không nghèo): Mã hóa là 0.
ho ngheo(nghèo): Mã hóa là 1.

Điều này cho thấy trong hồi quy logistic, biến phụ thuộc “tình trạng nghèo” được mã hóa dưới dạng nhị phân với 0 đại diện cho các hộ gia đình “không nghèo” và 1 cho các hộ gia đình “nghèo”.

Block 0: Kết quả hồi quy không có biến độc lập

Phần tiếp theo của output được gọi là Block 0 (hoặc mô hình rỗng – “null model”), cung cấp kết quả của phân tích mà không có bất kỳ biến độc lập (predictor variables) nào được đưa vào mô hình. Đây là mô hình cơ bản, chỉ dựa trên biến phụ thuộc để dự đoán. Kết quả từ Block 0 sẽ được sử dụng làm điểm so sánh cho mô hình khi chúng ta thêm các biến độc lập (Block 1).

Ý nghĩa của Block 0:

Mô hình Block 0chỉ sử dụng tỷ lệ cơ sở của biến phụ thuộc (tình trạng nghèo) mà không tính đến bất kỳ yếu tố dự đoán nào.
Tỷ lệ dự đoán cơ bảnlà dự đoán dựa trên việc chọn nhóm phổ biến hơn của biến phụ thuộc (trong trường hợp này, có thể là “không nghèo”).
Kết quả từ Block 0 sẽ cho thấy mô hình đơn giản nhất có thể hoạt động như thế nào mà không cần sử dụng bất kỳ thông tin nào từ các biến độc lập. Nó giúp chúng ta thấy mức độ cải thiện khi các biến độc lập được thêm vào mô hình ở Block 1.

So sánh với Block 1:

Khi các biến độc lập được thêm vào trong Block 1, chúng ta có thể so sánh độ chính xác của mô hình giữa hai khối để đánh giá xem các yếu tố dự đoán có làm tăng khả năng dự đoán tình trạng nghèo hay không.
Nếu mô hình với các biến độc lập trong Block 1 có độ chính xác cao hơn so với Block 0, điều đó chứng tỏ rằng các biến độc lập có đóng góp quan trọng vào khả năng dự đoán tình trạng nghèo của mô hình.

Vì Block 0 chỉ là mô hình rỗng, nó sẽ không thể đưa ra các dự đoán chính xác như mô hình hồi quy logistic đầy đủ với các yếu tố dự đoán (Block 1). Kết quả sẽ chỉ ra tầm quan trọng của việc sử dụng các biến độc lập trong mô hình hồi quy logistic.

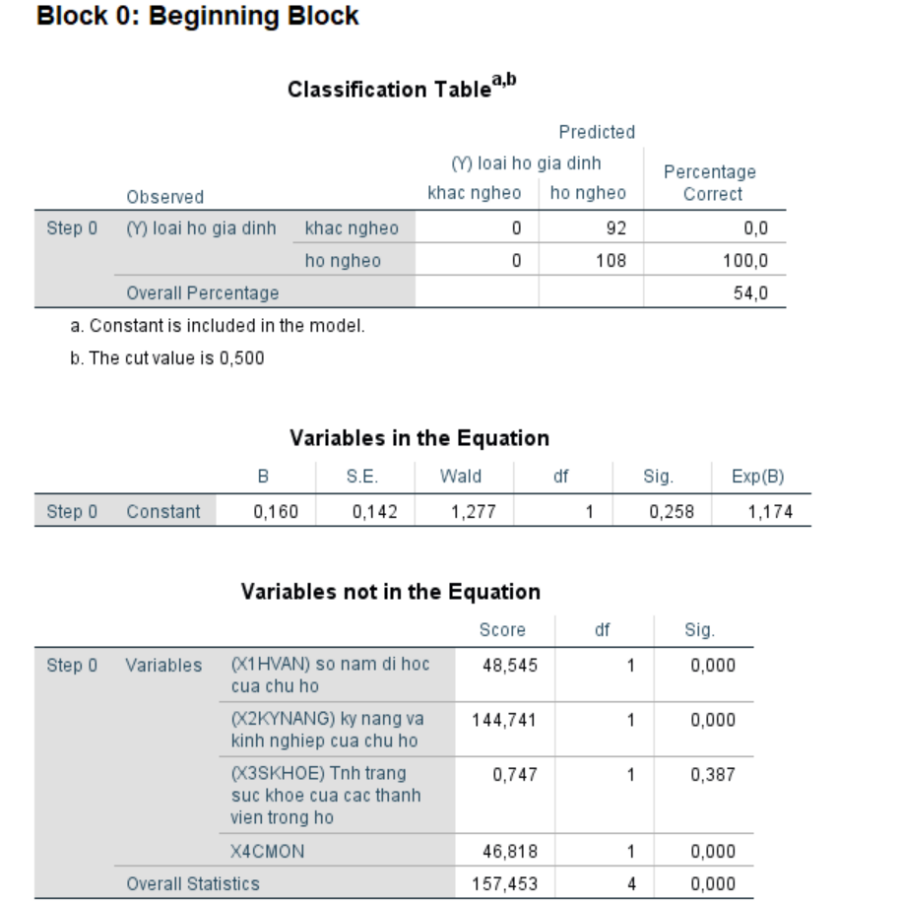
Block 1: Phương pháp Enter

Khi các biến độc lập (predictor variables) được đưa vào mô hình trong Block 1, phần mềm sẽ kiểm tra mức độ phù hợp của mô hình hồi quy logistic đã xây dựng, sử dụng các chỉ số Goodness-of-fit để đánh giá xem mô hình có mô tả tốt dữ liệu hay không. Một trong những kiểm định chính được sử dụng để đánh giá sự phù hợp của mô hình là Omnibus Test of Model Coefficients.

Omnibus Test of Model Coefficients:

Omnibus Test of Model Coefficients là một bước quan trọng để đánh giá sự phù hợp tổng thể của mô hình. Nếu kiểm định này có ý nghĩa (p < 0.05), điều đó cho thấy rằng các biến độc lập thực sự có ý nghĩa trong việc giải thích hoặc dự đoán biến phụ thuộc và mô hình hồi quy logistic có thể được coi là “phù hợp tốt” với dữ liệu khảo sát.

Mục đích: Kiểm định này được sử dụng để đánh giá độ phù hợp của mô hình khi có sự tham gia của các biến độc lập so với mô hình rỗng (Block 0). Nếu mô hình có biến độc lập (Block 1) cải thiện đáng kể so với mô hình không có biến nào (Block 0), điều này cho thấy mô hình đã tốt hơn và các biến độc lập có ý nghĩa trong việc giải thích biến phụ thuộc.

Giả thuyết:

H0: Mô hình mới không tốt hơn so với mô hình rỗng (không có biến độc lập nào ảnh hưởng đến biến phụ thuộc).
H1: Mô hình mới tốt hơn so với mô hình rỗng, tức là có sự cải thiện đáng kể khi đưa các biến độc lập vào mô hình.

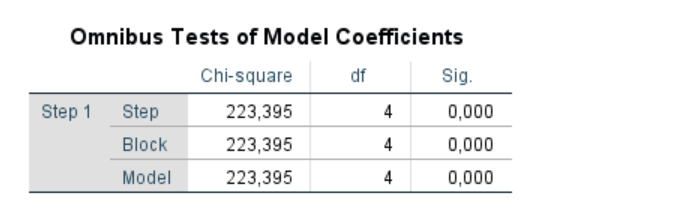
Các đọc kết quả: Kết quả kiểm định giả thuyết về mức độ phù hợp của mô hình tổng quát có mức ý nghĩa < 0.05. Như vậy mô hình tổng quát cho thấy có sự tương quan giữa biến phụ thuộc và các biến độc lập có ý nghĩa thống kê với khoảng tin cậy trên 99% và mô hình được chọn là phù hợp. Điều này đồng nghĩa với việc có sự cải thiện đáng kể trong khả năng dự đoán của mô hình khi các yếu tố như Trình độ chuyên môn, Học vấn, Sức khỏe, và Kỹ năng cụ thể được thêm vào.

Hosmer and Lemeshow Test

Kiểm định Hosmer-Lemeshow cũng được sử dụng để đánh giá độ phù hợp của mô hình hồi quy logistic. Đây là một kiểm định quan trọng để xem xét sự khác biệt giữa các giá trị dự đoán từ mô hình và giá trị quan sát thực tế trong dữ liệu.

Mục đích: Kiểm định này so sánh tần suất dự đoán từ mô hình hồi quy logistic với tần suất thực tế từ dữ liệu, nhằm xem mô hình có khớp tốt với dữ liệu hay không.

Nếu p-value của kiểm định Hosmer-Lemeshow lớn hơn 0.05, mô hình được cho là phù hợp với dữ liệu. Điều này có nghĩa là không có sự khác biệt đáng kể giữa giá trị dự đoán từ mô hình và giá trị quan sát thực tế.

Nếu p-value nhỏ hơn 0.05, mô hình có thể không phù hợp với dữ liệu, tức là có sự khác biệt đáng kể giữa giá trị dự đoán và giá trị thực tế.

Giả thuyết:

H0 (giả thuyết không): Không có sự khác biệt giữa các giá trị dự đoán từ mô hình và các giá trị quan sát thực tế.
H1 (giả thuyết đối): Có sự khác biệt đáng kể giữa các giá trị dự đoán và quan sát.

Cách đọc kết quả: Kết quả cho thấy kiểm định Hosmer-Lemeshow có p-value = 0,999 > 0.05: Điều này cho thấy mô hình hồi quy logistic phù hợp tốt với dữ liệu. Không có sự khác biệt đáng kể giữa giá trị dự đoán của mô hình và giá trị thực tế từ dữ liệu khảo sát.Điều đó có nghĩa là mô hình hồi quy logistic đang khớp tốt với dữ liệu thực tế, và các yếu tố độc lập trong mô hình (ví dụ: Trình độ chuyên môn, Học vấn, Sức khỏe, Kỹ năng cụ thể) có khả năng dự đoán tình trạng nghèo của hộ gia đình một cách hiệu quả.

Contingency Table cho kiểm định Hosmer-Lemeshow:

Bảng dự phòng (Contingency Table) trong kiểm định Hosmer-Lemeshow được sử dụng để so sánh sự khác biệt giữa các giá trị quan sát thực tế (observed values) và các giá trị dự đoán (predicted values) từ mô hình hồi quy logistic. Mục tiêu của bảng này là đánh giá xem mô hình có khớp tốt với dữ liệu thực tế hay không, thông qua việc kiểm tra sự tương đồng giữa hai nhóm giá trị này.

Bảng dự phòng chia dữ liệu thành các nhóm dựa trên xác suất dự đoán của mô hình.

Observed values: Đây là số lượng trường hợp thực tế (theo dữ liệu khảo sát) nằm trong mỗi nhóm dự đoán (ví dụ, số hộ nghèo và không nghèo thực sự trong mỗi nhóm).

Predicted values: Đây là số lượng trường hợp mà mô hình hồi quy dự đoán sẽ nằm trong các nhóm đó (dựa trên các biến độc lập trong mô hình).

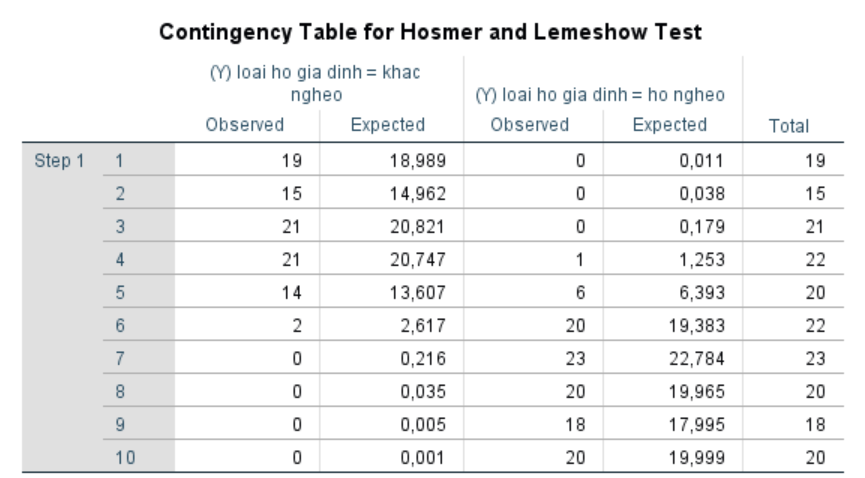
Cách đọc kết quả:

Đối với mỗi bước (Step), các giá trị Observed và Expected trong cột “loại hộ gia đình = khác nghèo” và “loại hộ gia đình = hộ nghèo” là rất gần nhau.

Ví dụ:

Ở Step 1, có 19 hộ gia đình thực tế được phân loại là “khác nghèo” (Observed) và mô hình dự đoán có 18,989 hộ gia đình sẽ thuộc loại này (Expected), trong khi số hộ nghèo dự đoán là 0,011 nhưng không có hộ nào thực tế thuộc nhóm này.
Ở Step 10, không có hộ nào thuộc loại “khác nghèo” trong dữ liệu thực tế và mô hình cũng dự đoán rất thấp với giá trị kỳ vọng là 0,001. Tương tự, số lượng hộ nghèo thực tế là 20 và dự đoán cũng là 19,999, rất gần với nhau.

Các giá trị Observed và Expected trong từng bước đều rất gần nhau, điều này cho thấy mô hình đang phù hợp tốt với dữ liệu thực tế. Do đó, kiểm định Hosmer-Lemeshow sẽ cho thấy rằng không có sự khác biệt đáng kể giữa các giá trị quan sát và dự đoán, và mô hình hồi quy logistic có thể được coi là phù hợp với dữ liệu. Kết quả này hỗ trợ kết luận rằng các yếu tố độc lập trong mô hình (như Trình độ chuyên môn, Học vấn, Sức khỏe, Kỹ năng cụ thể) là những biến dự đoán hiệu quả cho tình trạng nghèo của hộ gia đình.

Tóm tắt mô hình (Model Summary):

Phần Model Summary trong kết quả hồi quy logistic đưa ra các chỉ số Pseudo R-Square để đánh giá mức độ giải thích của mô hình đối với biến phụ thuộc. Tuy nhiên, đây không phải là R-Square như trong hồi quy tuyến tính, mà là các giá trị gần đúng nhằm ước lượng mức độ biến động của biến phụ thuộc (criterion variable) có thể được giải thích bởi các biến độc lập trong mô hình.

Pseudo R-Square:

Pseudo R-Square không thể hiện rõ ràng mức độ biến thiên được giải thích, như cách mà R-Square trong hồi quy tuyến tính làm.

Tuy nhiên, nó vẫn có thể được sử dụng như một phương tiện để so sánh các mô hình hoặc để đưa ra ước lượng về sự biến thiên mà mô hình giải thích.

Nagelkerke’s R-Square:

Nagelkerke’s R-Square là một phiên bản điều chỉnh của Cox & Snell R-Square, điều chỉnh quy mô của thống kê để bao trùm toàn bộ phạm vi từ 0 đến 1.

Nagelkerke’s R-Square thường được sử dụng nhiều hơn vì nó dễ diễn giải hơn và có giá trị trong khoảng từ 0 đến 1, tương tự như R-Square trong hồi quy tuyến tính.

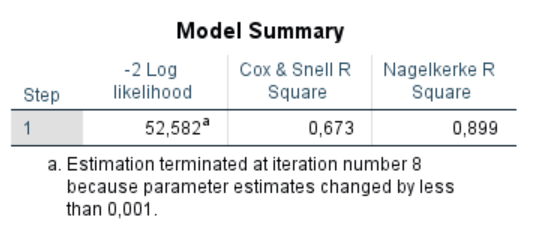
Cách đọc kết quả:

Trong trường hợp này, giá trị Nagelkerke’s R-Square là 0.899 (89.9%), điều này có nghĩa là 89.9% sự thay đổi trong biến phụ thuộc (tình trạng nghèo của hộ gia đình) có thể được giải thích bởi các biến độc lập trong mô hình, như trình độ chuyên môn, học vấn, sức khỏe và kỹ năng cụ thể của chủ hộ. Điều này cho thấy mô hình có độ phù hợp tương đối tốt để dự đoán tình trạng nghèo của các hộ gia đình dựa trên các yếu tố được phân tích.

Bảng Phân loại (Classification Table):

Bảng Phân loại (Classification Table) trong kết quả hồi quy logistic cung cấp thông tin về mức độ chính xác của mô hình trong việc dự đoán chính xác các trường hợp khi thêm các biến độc lập vào phân tích. Nó cho biết mô hình đã dự đoán chính xác bao nhiêu phần trăm các trường hợp thuộc về nhóm nào (ví dụ: “khác nghèo” hoặc “hộ nghèo”).

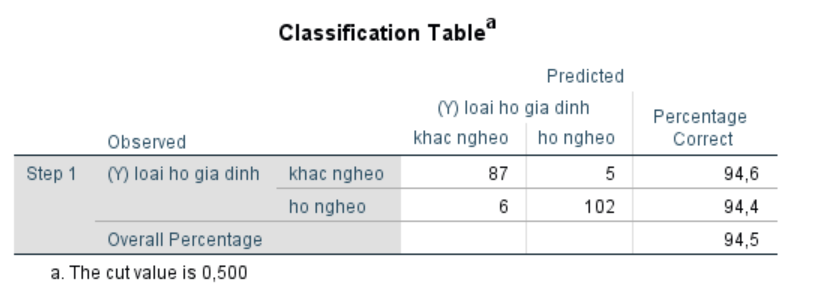
Cách đọc kết quả:

Hàng đầu tiên (“khác nghèo”):

87trường hợp thuộc nhóm “khác nghèo” được dự đoán chính xác bởi mô hình.
5trường hợp thuộc nhóm “khác nghèo” bị mô hình dự đoán sai, xếp vào nhóm “hộ nghèo”.
Tỷ lệ chính xác của nhóm “khác nghèo” là 94.6%.

Hàng thứ hai (“hộ nghèo”):

102trường hợp thuộc nhóm “hộ nghèo” được mô hình dự đoán chính xác.
6trường hợp thuộc nhóm “hộ nghèo” bị mô hình dự đoán sai, xếp vào nhóm “khác nghèo”.
Tỷ lệ chính xác của nhóm “hộ nghèo” là 94.4%.

Tỷ lệ chính xác tổng thể:

5%trường hợp được mô hình dự đoán chính xác (kết hợp cả “khác nghèo” và “hộ nghèo”).

Mô hình hồi quy logistic đã phân loại chính xác 94.5% tổng số trường hợp, còn được gọi là percentage accuracy in classification (PAC). Điều này có nghĩa là:

Mô hình dự đoán chính xác 94.5%các trường hợp thuộc vào nhóm “khác nghèo” hoặc “hộ nghèo” dựa trên các biến độc lập như trình độ chuyên môn, học vấn, sức khỏe, và kỹ năng cụ thể của chủ hộ.
Đây là một chỉ số quan trọng cho thấy khả năng dự đoáncủa mô hình đã cải thiện rõ rệt sau khi thêm các biến dự đoán so với mô hình Block 0 ban đầu.

Trong kết quả hồi quy logistic, các chỉ số Specificity và Sensitivity cung cấp cái nhìn sâu sắc về khả năng dự đoán của mô hình đối với các nhóm cụ thể của biến phụ thuộc.Cả Specificity và Sensitivity đều khá cao, với mức chính xác tương tự cho cả hai nhóm (94.6% cho nhóm “khác nghèo” và 94.4% cho nhóm “hộ nghèo”).

Biến trong phương trình (Variables in the Equation)

Biến trong phương trình (Variables in the Equation) cung cấp thông tin chi tiết về mối quan hệ giữa các biến dự báo (predictors) và kết quả (outcome).

Odds (Tỷ lệ odds):

Tỷ lệ odds là tỷ số giữa xác suất xảy ra sự kiện A (P(A)) và xác suất không xảy ra sự kiện đó (P(B)).
Công thức: P(A)/P(B).

B (Hệ số Beta):

Blà sự thay đổi dự đoán trong log odds: khi biến dự báo thay đổi 1 đơn vị, sẽ có sự thay đổi theo giá trị Exp(B) trong xác suất xảy ra của biến kết quả.
Hệ số beta có thể có giá trị âm hoặc dương, và mỗi hệ số beta đều có một giá trị tkèm theo mức ý nghĩa (significance) của giá trị t đó.
Nếu hệ số beta là âm, điều này có nghĩa là: với mỗi sự tăng 1 đơn vị trong biến dự báo, biến kết quả sẽ giảmtheo giá trị của hệ số beta.

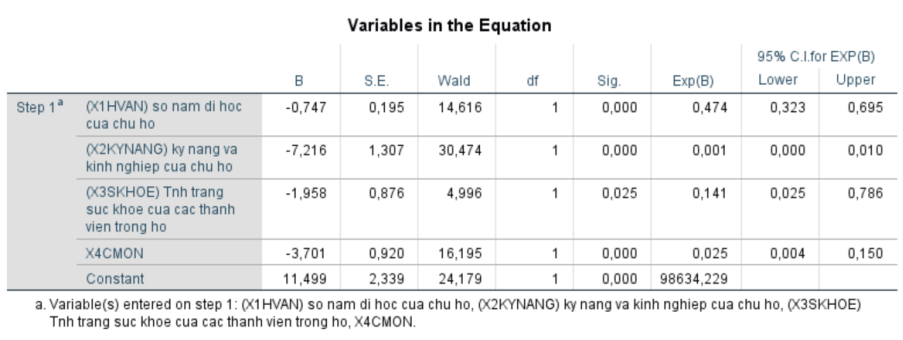
Dưới đây là phần giải thích từng cột trong bảng:

Cột B: Đây là hệ số hồi quy (B), biểu diễn ảnh hưởng của từng biến độc lập lên biến phụ thuộc. Hệ số dương cho thấy biến độc lập có ảnh hưởng tích cực, trong khi hệ số âm cho thấy tác động tiêu cực.

Cột S.E. (Standard Error): Đây là sai số chuẩn của hệ số B, cho thấy mức độ biến động của ước lượng hệ số.

Cột Wald: Đây là chỉ số thống kê Wald, dùng để kiểm tra xem liệu hệ số hồi quy có khác 0 một cách có ý nghĩa thống kê hay không.

Cột df (Degrees of Freedom): Bậc tự do của từng hệ số trong mô hình.

Cột Sig. (Significance): Đây là giá trị p, cho thấy mức độ ý nghĩa thống kê. Nếu Sig. nhỏ hơn 0.05, thì biến đó có ảnh hưởng đáng kể lên mô hình.

Cột Exp(B): Đây là tỷ số Odds Ratio, biểu diễn mức thay đổi của tỷ lệ odds khi biến độc lập tăng một đơn vị.

Cột 95% C.I.for EXP(B): Đây là khoảng tin cậy 95% của giá trị Exp(B), thể hiện mức độ biến động của tỷ số Odds trong khoảng tin cậy này.

Cách đọc kết quả:

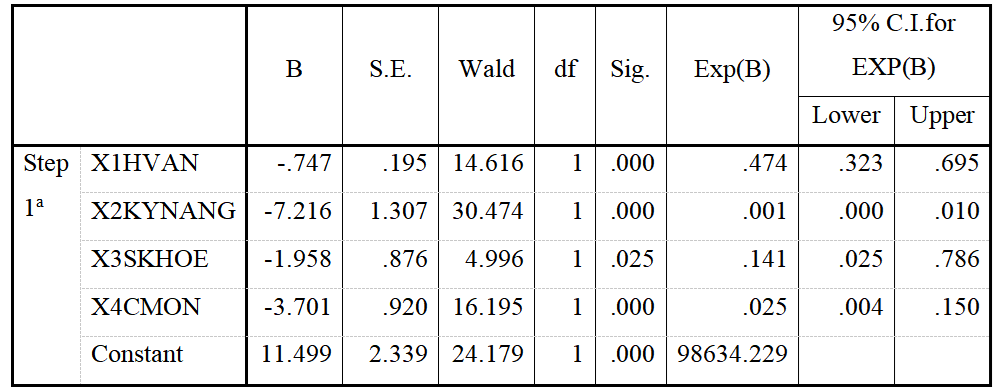
Nhìn vào bảng … ta thấy giá trị Sig. của các biến học vấn chủ hộ (sig. = 0.000); kỹ năng cụ thể của chủ hộ (sig. = 0.000); sức khỏe (sig. = 0.025); trình độ chuyên môn (sig. = 0.000) < 0.05 (5%). Vì vậy, mối liên hệ giữa các biến độc lập trong mô hình và biến hộ nghèo có ý nghĩa thống kê với mức tin cậy chung là 95%.

Dấu của các hệ số trong mô hình hồi quy Binary logistic phù hợp với mong đợi.

Biến số “Học vấn chủ hộ (X1)” có hệ số b_X1 = – 0.747, có ý nghĩa thống kê ở mức 5% (sig. = 0.000), tương quan trái chiều với tình trạng nghèo của hộ gia đình. Biến này có tác động mạnh thứ tư đến tình trạng nghèo của hộ gia đình trong mô hình hồi quy. Trình độ học vấn thấp đã làm hạn chế khả năng tiếp thu các phương pháp sản xuất mới, hạn chế việc lựa chọn phương án đầu tư sao cho có hiệu quả, hạn chế khả năng nhận biết thông tin giá cả thị trường. Trình độ học vấn thấp của chủ hộ còn ảnh hưởng lâu dài cho các thế hệ sau. Những người nghèo có trình độ học vấn thấp, ít có cơ hội kiếm được việc làm tốt, ổn định. Mức thu nhập của họ hầu như chỉ bảo đảm nhu cầu dinh dưỡng tối thiểu và do vậy, họ không có điều kiện để nâng cao trình độ của mình trong tương lai để thoát khỏi cảnh nghèo khó.

Biến số “Kỹ năng cụ thể (X2)” có hệ số b_X2 = – 7.216, có ý nghĩa thống kê ở mức 5% (sig. = 0.000), tương quan trái chiều với tình trạng nghèo của hộ gia đình. Biến này có tác động mạnh nhất đến tình trạng nghèo của hộ gia đình trong mô hình hồi quy. Người nghèo là những đối tượng ít được tiếp cận với các nguồn lực về khoa học công nghệ. Họ không có điều kiện để áp dụng những tiến bộ của Khoa học kỹ thuật vào sản xuất. Hỗ trợ áp dụng khoa học và công nghệ trong sản xuất cho người nghèo là một trong những giải pháp để cải thiện đầu ra của thu nhập.

Biến số “Sức khỏe (X3)” có hệ số b_X1 = – 1.958, có ý nghĩa thống kê ở mức 5% (sig. = 0.025), tương quan trái chiều với tình trạng nghèo của hộ gia đình. Biến này có tác động mạnh thứ ba đến tình trạng nghèo của hộ gia đình trong mô hình hồi quy. Những chủ hộ có vấn đề về sức khỏe thường ít có khả năng lao động và vì vậy thường không có khả năng để tạo ra thu nhập. Bệnh tật và sức khoẻ kém ảnh hưởng trực tiếp đến thu nhập và chi tiêu của người nghèo, làm cho người nghèo rơi vào vòng luẩn quẩn của đói nghèo. Vì vây, việc cải thiện sức khoẻ cho người nghèo là một trong những yếu tố cơ bản nhất để người nghèo tự vươn lên thoát khỏi cảnh nghèo khó.

Biến số “Trình độ chuyên môn (X4)” có hệ số b_X4 = – 3.701, có ý nghĩa thống kê ở mức 5% (sig. = 0.000), tương quan trái chiều với tình trạng nghèo của hộ gia đình. Biến này có tác động mạnh thứ hai đến tình trạng nghèo của hộ gia đình trong mô hình hồi quy. Từ trình độ học vấn và chuyên môn quá thấp, dẫn đến tình trạng hoạt động của người nghèo có phần kém năng động, hiệu quả. Trong thời đại kinh tế thị trường, với sự tập trung một nguồn lao động lớn tại Tp.Bến Tre và các huyện lân cận, để có được những công việc thu nhập ổn định thì trình độ chuyên môn là một trong những cánh cửa quan trọng.