Tính phân phối chuẩn Phân phối xác suất đối xứng quanh giá trị trung bình, cho thấy rằng dữ liệu gần giá trị trung bình xuất hiện với tần suất cao hơn so với dữ liệu cách xa giá trị trung bình.
Tính phân phối chuẩn được đánh giá dựa trên:
- Độ lệch(Skewness)
- Độ nhọn(Kurtosis)
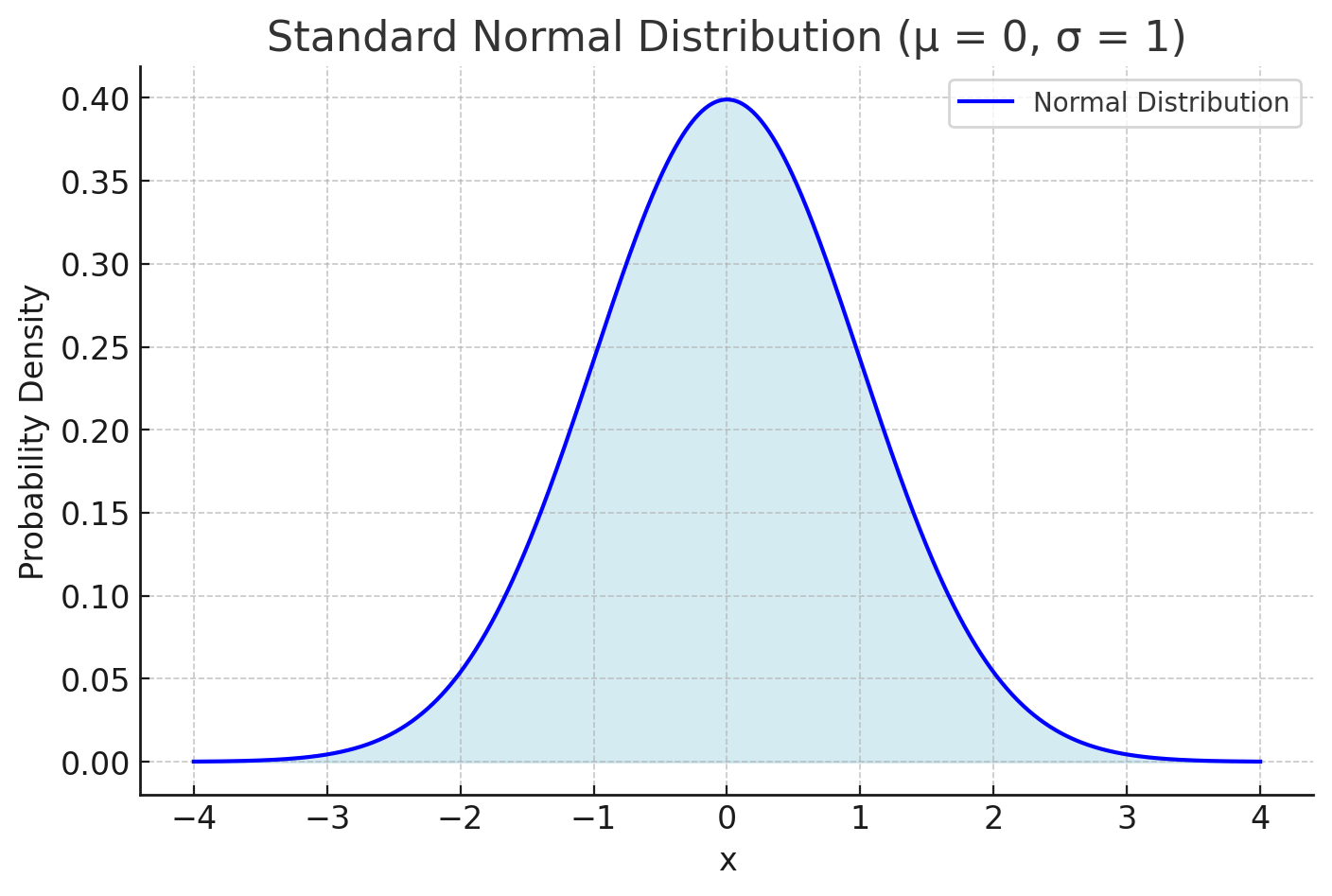
Độ lệch và Độ nhọn
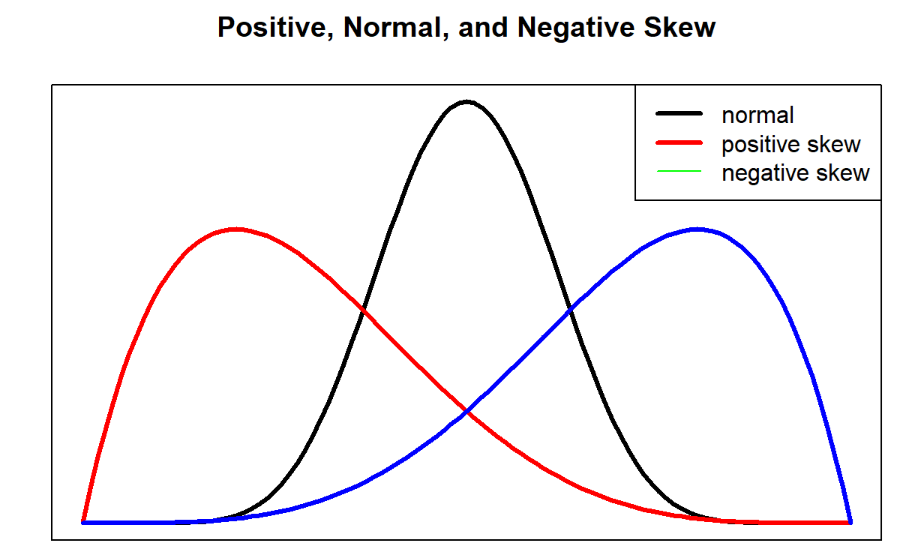
- Độ lệch(Skewness) – Là độ nghiêng của phân phối, có thể nghiêng về bên trái hoặc bên phải (như trong đồ thị trên của hình).
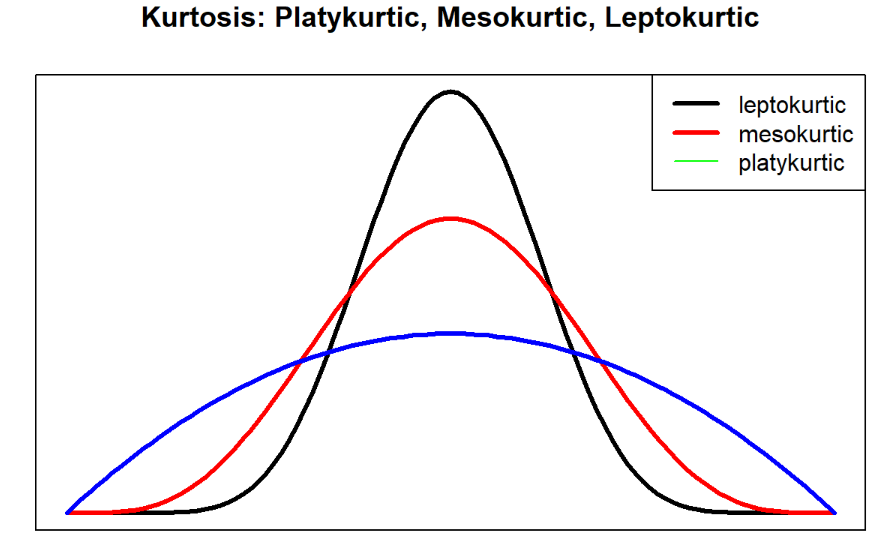
- Độ nhọn(Kurtosis) – Là mức độ nhọn của phân phối. Sự nặng hoặc nhẹ ở phần đuôi thường ám chỉ rằng dữ liệu của bạn trông phẳng hơn (hoặc ít phẳng hơn) so với phân phối chuẩn (như trong phần dưới của hình).
Đánh giá Tính Phân Phối Chuẩn
Đánh giá tính phân phối chuẩn được thực hiện bằng cách xem xét độ lệch của từng biến. Giá trị tuyệt đối của độ lệch (skewness) từ 1.0 trở xuống cho thấy dữ liệu có phân phối chuẩn. Tuy nhiên, trong phân tích mô hình cấu trúc tuyến tính (SEM) sử dụng ước lượng hợp lý tối đa (Maximum Likelihood Estimator – MLE) như AMOS, mô hình khá bền vững với độ lệch lớn hơn 1.0 (tính theo giá trị tuyệt đối) nếu kích thước mẫu đủ lớn và vùng tới hạn (CR) của độ lệch không vượt quá 8.0.
Điều này có nghĩa là, nhà nghiên cứu vẫn có thể tiếp tục phân tích thêm (SEM) khi ước lượng sử dụng MLE. Thông thường, kích thước mẫu lớn hơn 200 được coi là đủ lớn khi sử dụng MLE, ngay cả khi phân phối dữ liệu có hơi lệch khỏi chuẩn. Do đó, với kích thước mẫu lớn hơn 200, nhà nghiên cứu có thể tiếp tục phân tích khi độ lệch tuyệt đối nằm trong khoảng +/-2, mặc dù một số chuyên gia đề xuất khoảng +/-3.
Một phương pháp khác để đánh giá tính phân phối chuẩn là xem xét thống kê độ nhọn (kurtosis). Tuy nhiên, SEM sử dụng MLE cũng khá bền vững với các vi phạm độ nhọn của phân phối chuẩn đa biến nếu kích thước mẫu đủ lớn. Đối với độ nhọn, khoảng từ -10 đến +10 vẫn được coi là phân phối chuẩn (Collier, 2020). Dựa trên kết quả của chúng tôi, có thể thấy rằng cả độ lệch và độ nhọn đều nằm trong phạm vi chấp nhận được để được coi là “chuẩn”.
Không Đáp Ứng Giả Định Phân Phối Chuẩn
Tóm lại, trong trường hợp giả định phân phối chuẩn không được thỏa mãn, nhà nghiên cứu vẫn có nhiều lựa chọn khác nhau. Một trong số đó là loại bỏ các biến không đạt chuẩn (dựa trên độ lệch) khỏi mô hình đo lường và tiếp tục phân tích.
Một lựa chọn khác là loại bỏ các quan sát cách xa trung tâm của phân phối (quan sát ngoại lệ).
Tuy nhiên, phương pháp phổ biến nhất gần đây là tiếp tục phân tích với MLE mà không cần loại bỏ bất kỳ biến nào hoặc loại bỏ quan sát nào, và xác nhận lại kết quả phân tích thông qua phương pháp Bootstrapping.
Bootstrapping là quá trình lấy mẫu lại từ tập dữ liệu hiện có bằng cách lấy mẫu có hoàn lại. Phương pháp thống kê này sẽ tính toán giá trị trung bình và độ lệch chuẩn cho từng mẫu với kích thước n để tạo ra phân phối mẫu mới.
Nhà nghiên cứu có thể yêu cầu Amos thu thập 1000 mẫu ngẫu nhiên từ tập dữ liệu và thực hiện lại phân tích. Do kích thước mẫu lớn (1000), phân phối mẫu mới sẽ gần với phân phối chuẩn hơn. Amos sẽ phân tích dữ liệu Bootstrapping và tạo ra các khoảng tin cậy cũng như mức ý nghĩa cho từng tham số liên quan đến phân tích.
Nhà nghiên cứu có thể so sánh kết quả thực tế với kết quả từ Bootstrapping để xác nhận phân tích. Nếu kết quả có sự khác biệt, kết quả từ Bootstrapping sẽ được chấp nhận.
Hướng dẫn đánh giá phân phối chuẩn cho dữ liệu trên AMOS
Khi đánh giá mô hình CFA, trong thẻ Output chọn Test for normality and outliers để đánh giá phân phối chuẩn cho mỗi biến trong bộ dữ liệu
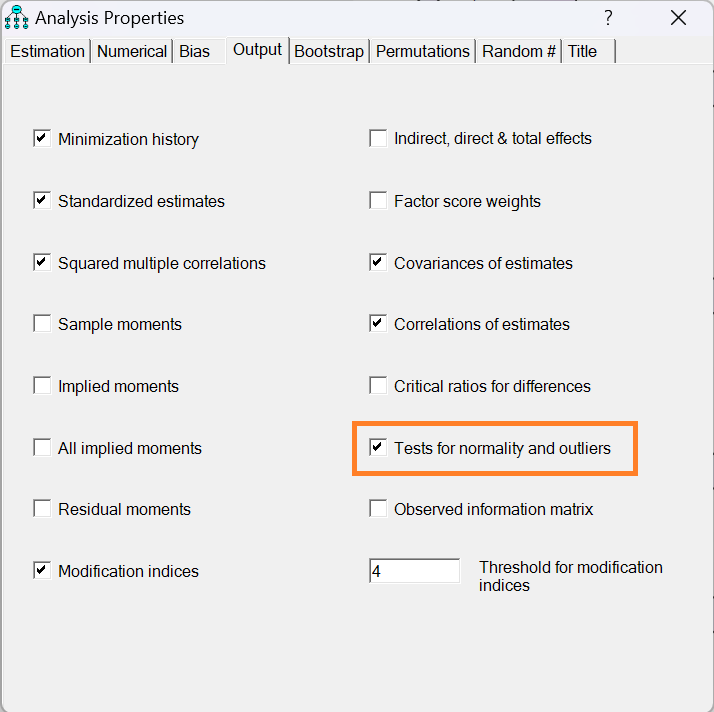
Bảng bên dưới trình bày kết quả từ quy trình nêu trên. Bảng trình bày đánh giá tính phân phối chuẩn cho tất cả các câu hỏi liên quan đến mô hình đo lường.
Tiếp tục đọc kết quả (Assessment of normality)
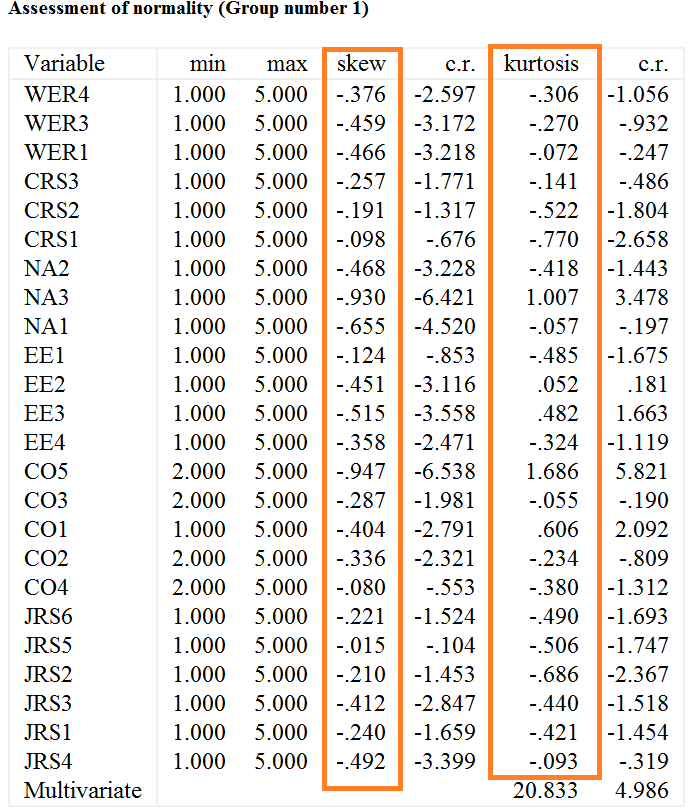
Theo Kline (2015) nếu giá trị tuyệt đối của Skew là 2 hoặc thấp hơn 3 thì dữ liệu được phân phối chuẩn. Một phươn pháp khác để đánhgá phân phối chuẩn là xem giá trị tuyệtđối của kurtosis bé hơn hoặc băng 10. Như bảng mô tả từ AMOS, các giá trị tuyệt đối của skewness cho tất cả các câu hỏi đo lường lớn nhất là 0.947 (<3) trong khi các giá trị tuyệt đố của kurtosis lớn nhất là 1.686 (<10). Điều này xác nhận tính phân phối chuẩn cho các câu hỏi đo lường trong mô hình.
Nguồn tham khảo:
Collier, J. E. (2020). Applied structural equation modeling using AMOS: Basic to advanced techniques. Routledge.







