Công thức Cochran là gì?

Trong bất kỳ nghiên cứu định lượng nào, việc xác định cỡ mẫu (sample size) phù hợp là một bước nền tảng, quyết định tính chính xác, độ tin cậy và khả năng khái quát hóa của kết quả nghiên cứu cho tổng thể (population). Một cỡ mẫu quá nhỏ có thể dẫn đến kết luận sai lệch, trong khi cỡ mẫu quá lớn lại gây lãng phí tài nguyên (thời gian, chi phí). Công thức Cochran là một trong những phương pháp thống kê được sử dụng rộng rãi và hiệu quả nhất để ước tính cỡ mẫu cần thiết, đặc biệt khi nghiên cứu tập trung vào việc ước lượng tỷ lệ (proportion) trong một tổng thể lớn hoặc chưa biết kích thước chính xác.

Công thức Cochran là một phương pháp thống kê được sử dụng để xác định kích thước mẫu tối ưu trong các nghiên cứu định lượng, đảm bảo độ tin cậy và độ chính xác của kết quả. Được phát triển bởi William G. Cochran, công thức này đặc biệt hữu ích khi nghiên cứu dân số lớn hoặc không biết chính xác kích thước dân số.

Tại sao công thức Cochran quan trọng?

• Độ tin cậy cao: Giúp đảm bảo kết quả nghiên cứu đại diện cho dân số.
• Tiết kiệm tài nguyên: Xác định kích thước mẫu vừa đủ, tránh lãng phí thời gian và chi phí.
• Ứng dụng rộng rãi: Được sử dụng trong nhiều lĩnh vực như y học, kinh tế, giáo dục, và marketing.

Công thức Cochran và Cách tính

Công thức Cochran được biểu diễn như sau:

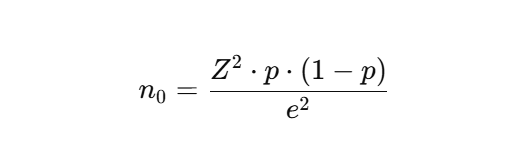
Trong đó:

• n₀: Kích thước mẫu cần tính.
• Z: Giá trị Z-score tương ứng với mức độ tin cậy (ví dụ: 1.96 cho mức tin cậy 95%). Giá trị Z-score tương ứng với mức độ tin cậy mong muốn. Đây là số độ lệch chuẩn mà một tỷ lệ mẫu có thể cách xa tỷ lệ tổng thể. Các giá trị Z phổ biến:

• Mức tin cậy 90% -> Z = 1.645
• Mức tin cậy 95% -> Z = 1.96 (Thường được sử dụng nhất)
• Mức tin cậy 99% -> Z = 2.576

• p: Tỷ lệ xảy ra của sự kiện (thường lấy 0.5 nếu không biết trước).
• q: 1 – p (thường là 0.5 nếu p = 0.5).
• e: Sai số biên mong muốn (Margin of Error hay Desired Precision). Đây là mức độ sai lệch tối đa chấp nhận được giữa tỷ lệ mẫu ước tính và tỷ lệ thực tế trong tổng thể. Thường được biểu thị dưới dạng số thập phân (ví dụ: 0.03 cho ±3%, 0.05 cho ±5%). Sai số biên càng nhỏ, cỡ mẫu yêu cầu càng lớn. Sai số cho phép thường là 0.05 hoặc 5%.

Các bước tính kích thước mẫu theo công thức Cochran

1. Xác định mức độ tin cậy: Chọn giá trị Z phù hợp (ví dụ: 1.96 cho 95%).
2. Ước lượng tỷ lệ p: Nếu không có dữ liệu trước, lấy p = 0.5 để tối đa hóa kích thước mẫu.
3. Xác định sai số e: Thông thường là 5% (0.05).
4. Áp dụng công thức: Thay các giá trị vào công thức để tính n₀.

Điều chỉnh cho dân số hữu hạn (nếu cần): Nếu dân số (N) nhỏ, sử dụng công thức điều chỉnh:

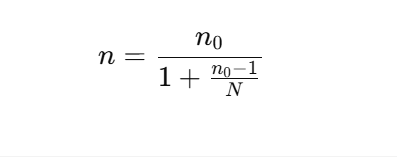
Ví dụ minh họa

Giả sử bạn muốn khảo sát ý kiến khách hàng về một sản phẩm với mức tin cậy 95% (Z = 1.96), sai số 5% (e = 0.05), và không biết tỷ lệ p (lấy p = 0.5, q = 0.5). Áp dụng công thức:

• $Z=1.96$

• $p=0.5$

• $e=0.05$

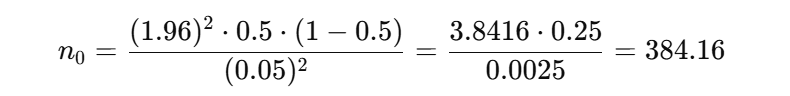
Kích thước mẫu cần là khoảng 384 khách hàng.

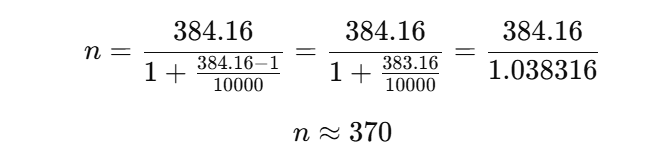
Vậy, kích thước mẫu cần là 370 khách hàng.

Ứng dụng của Công thức Cochran

Công thức Cochran được sử dụng rộng rãi trong nhiều lĩnh vực:

• Nghiên cứu thị trường: Xác định số lượng khách hàng cần khảo sát để đánh giá nhu cầu hoặc mức độ hài lòng.
• Y học: Tính kích thước mẫu cho các thử nghiệm lâm sàng hoặc nghiên cứu dịch tễ học.
• Giáo dục: Đánh giá hiệu quả của các chương trình đào tạo hoặc khảo sát ý kiến sinh viên.
• Xã hội học: Nghiên cứu hành vi hoặc thái độ của một nhóm dân số.

Lợi ích khi áp dụng

• Độ chính xác cao: Đảm bảo kết quả nghiên cứu phản ánh đúng đặc điểm dân số.
• Hiệu quả kinh tế: Giảm chi phí bằng cách tránh khảo sát mẫu quá lớn.
• Tính linh hoạt: Áp dụng được cho cả dân số lớn và nhỏ.

Những lưu ý khi sử dụng Công thức Cochran

• Ước lượng p chính xác: Nếu có dữ liệu trước, sử dụng tỷ lệ p thực tế để tăng độ chính xác.
• Chọn sai số hợp lý: Sai số nhỏ hơn (như 3%) sẽ yêu cầu mẫu lớn hơn, cần cân nhắc ngân sách.
• Kiểm tra dân số: Xác định xem dân số là hữu hạn hay vô hạn để áp dụng công thức điều chỉnh.
• Kiểm tra giả định: Công thức giả định mẫu ngẫu nhiên, cần đảm bảo quy trình chọn mẫu phù hợp.

Mẹo tối ưu khi sử dụng Công thức Cochran

• Sử dụng công cụ hỗ trợ: Các phần mềm như SPSS, R, hoặc Excel có thể tự động hóa quá trình tính toán.
• Tham khảo nghiên cứu trước: Tìm dữ liệu từ các nghiên cứu tương tự để ước lượng p chính xác hơn.
• Kiểm tra kết quả: Sau khi tính, đối chiếu với các phương pháp khác để đảm bảo tính hợp lý.
• Tài liệu tham khảo uy tín: Sử dụng các nguồn từ sách hoặc bài báo khoa học để hỗ trợ tính toán.

Tài liệu tham khảo

• Cochran, W. G. (1977). Sampling Techniques. John Wiley & Sons.
• Bài viết từ các trang uy tín như StatTrek, ResearchGate.

Công thức Cochran là công cụ mạnh mẽ giúp nhà nghiên cứu ước lượng được cỡ mẫu hợp lý, từ đó nâng cao độ tin cậy và tính đại diện cho nghiên cứu. Khi kết hợp với phần mềm phân tích dữ liệu như SPSS, bạn có thể triển khai các nghiên cứu định lượng một cách chuyên nghiệp, bài bản và khoa học hơn.

Bạn đã sẵn sàng áp dụng công thức Cochran cho nghiên cứu của mình? Hãy chia sẻ kinh nghiệm hoặc câu hỏi của bạn trong phần bình luận dưới đây! Đừng quên đăng ký nhận thêm tài liệu về thống kê và nghiên cứu từ chúng tôi.